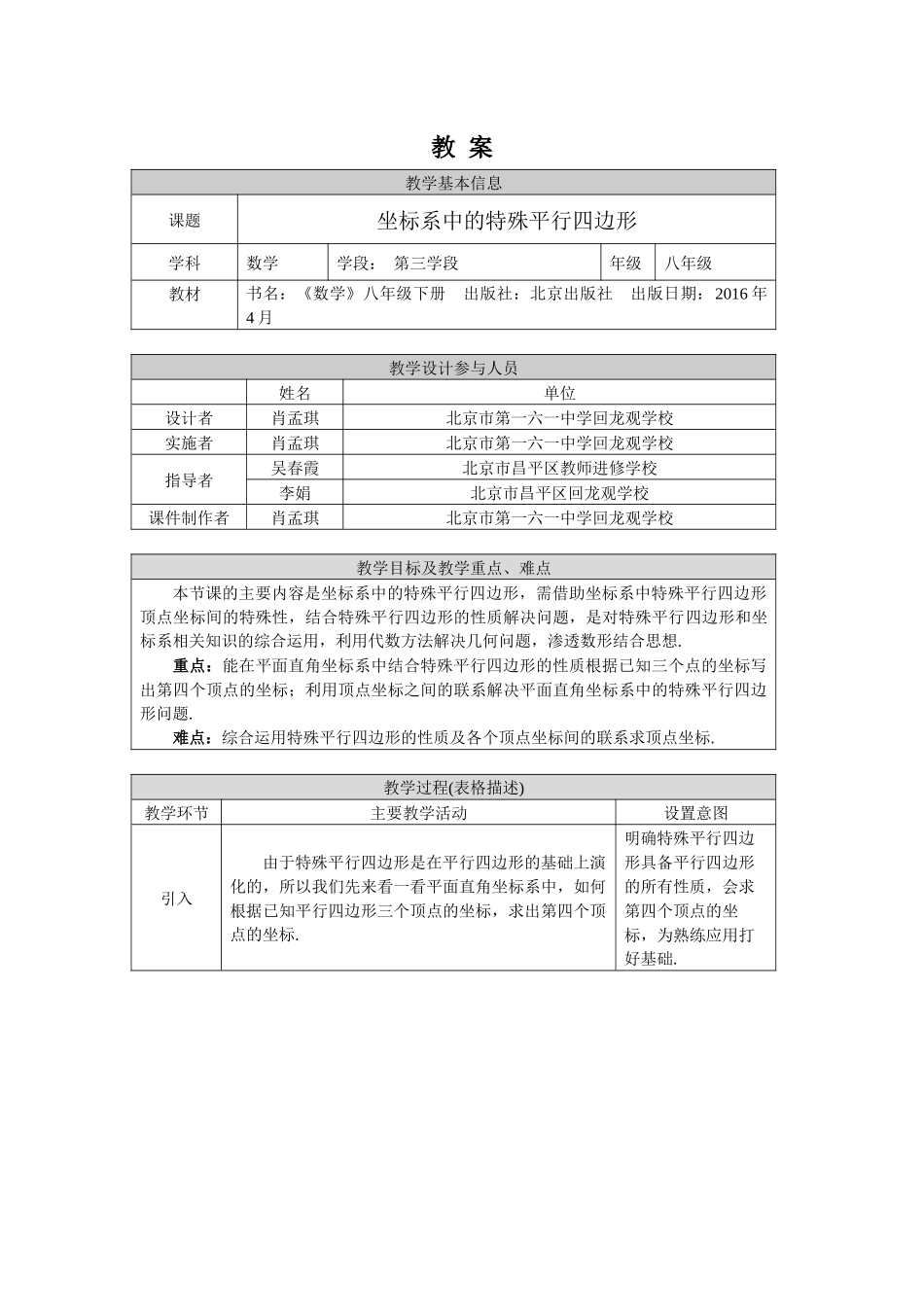
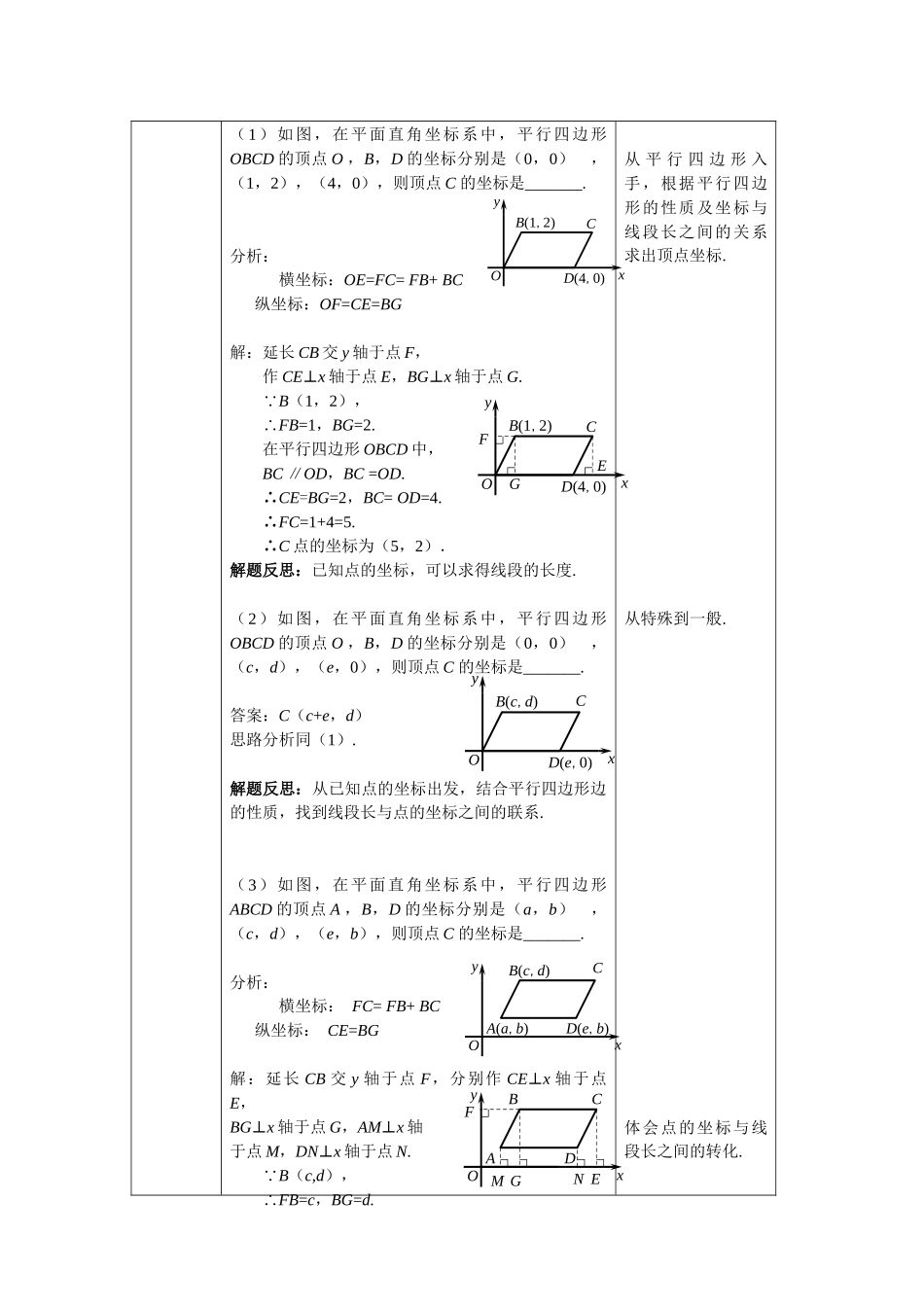
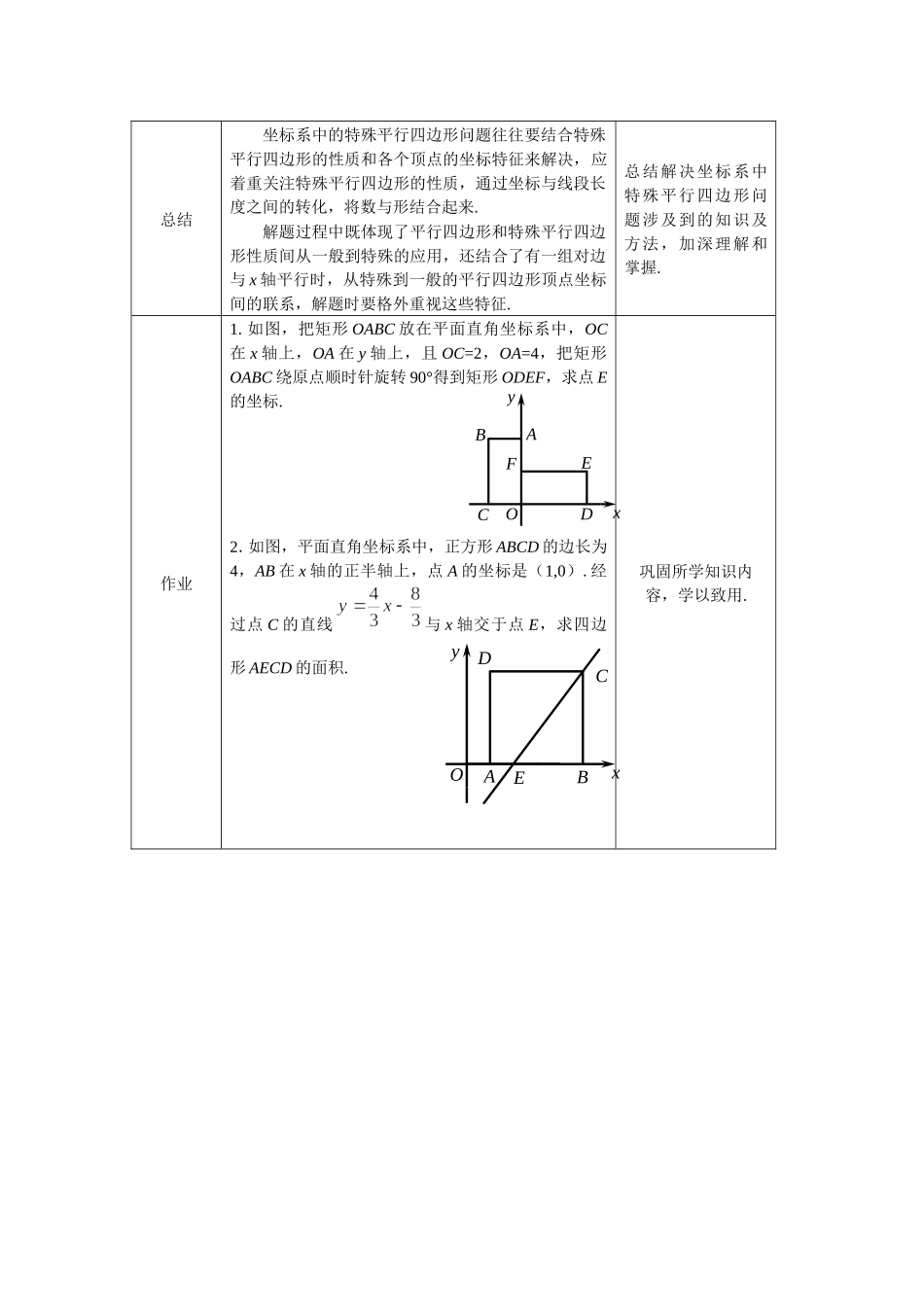
教案教学基本信息课题坐标系中的特殊平行四边形学科数学学段:第三学段年级八年级教材书名:《数学》八年级下册出版社:北京出版社出版日期:2016年4月教学设计参与人员姓名单位设计者肖孟琪北京市第一六一中学回龙观学校实施者肖孟琪北京市第一六一中学回龙观学校指导者吴春霞北京市昌平区教师进修学校李娟北京市昌平区回龙观学校课件制作者肖孟琪北京市第一六一中学回龙观学校教学目标及教学重点、难点本节课的主要内容是坐标系中的特殊平行四边形,需借助坐标系中特殊平行四边形顶点坐标间的特殊性,结合特殊平行四边形的性质解决问题,是对特殊平行四边形和坐标系相关知识的综合运用,利用代数方法解决几何问题,渗透数形结合思想.重点:能在平面直角坐标系中结合特殊平行四边形的性质根据已知三个点的坐标写出第四个顶点的坐标;利用顶点坐标之间的联系解决平面直角坐标系中的特殊平行四边形问题.难点:综合运用特殊平行四边形的性质及各个顶点坐标间的联系求顶点坐标.教学过程(表格描述)教学环节主要教学活动设置意图引入由于特殊平行四边形是在平行四边形的基础上演化的,所以我们先来看一看平面直角坐标系中,如何根据已知平行四边形三个顶点的坐标,求出第四个顶点的坐标.明确特殊平行四边形具备平行四边形的所有性质,会求第四个顶点的坐标,为熟练应用打好基础.(1)如图,在平面直角坐标系中,平行四边形OBCD的顶点O,B,D的坐标分别是(0,0),(1,2),(4,0),则顶点C的坐标是_______.分析:横坐标:OE=FC=FB+BC纵坐标:OF=CE=BG解:延长CB交y轴于点F,作CE⊥x轴于点E,BG⊥x轴于点G. B(1,2),∴FB=1,BG=2.在平行四边形OBCD中,BC∥OD,BC=OD.∴CE=BG=2,BC=OD=4.∴FC=1+4=5.∴C点的坐标为(5,2).解题反思:已知点的坐标,可以求得线段的长度.(2)如图,在平面直角坐标系中,平行四边形OBCD的顶点O,B,D的坐标分别是(0,0),(c,d),(e,0),则顶点C的坐标是_______.答案:C(c+e,d)思路分析同(1).解题反思:从已知点的坐标出发,结合平行四边形边的性质,找到线段长与点的坐标之间的联系.(3)如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(a,b),(c,d),(e,b),则顶点C的坐标是_______.分析:横坐标:FC=FB+BC纵坐标:CE=BG解:延长CB交y轴于点F,分别作CE⊥x轴于点E,BG⊥x轴于点G,AM⊥x轴于点M,DN⊥x轴于点N. B(c,d),∴FB=c,BG=d.从平行四边形入手,根据平行四...