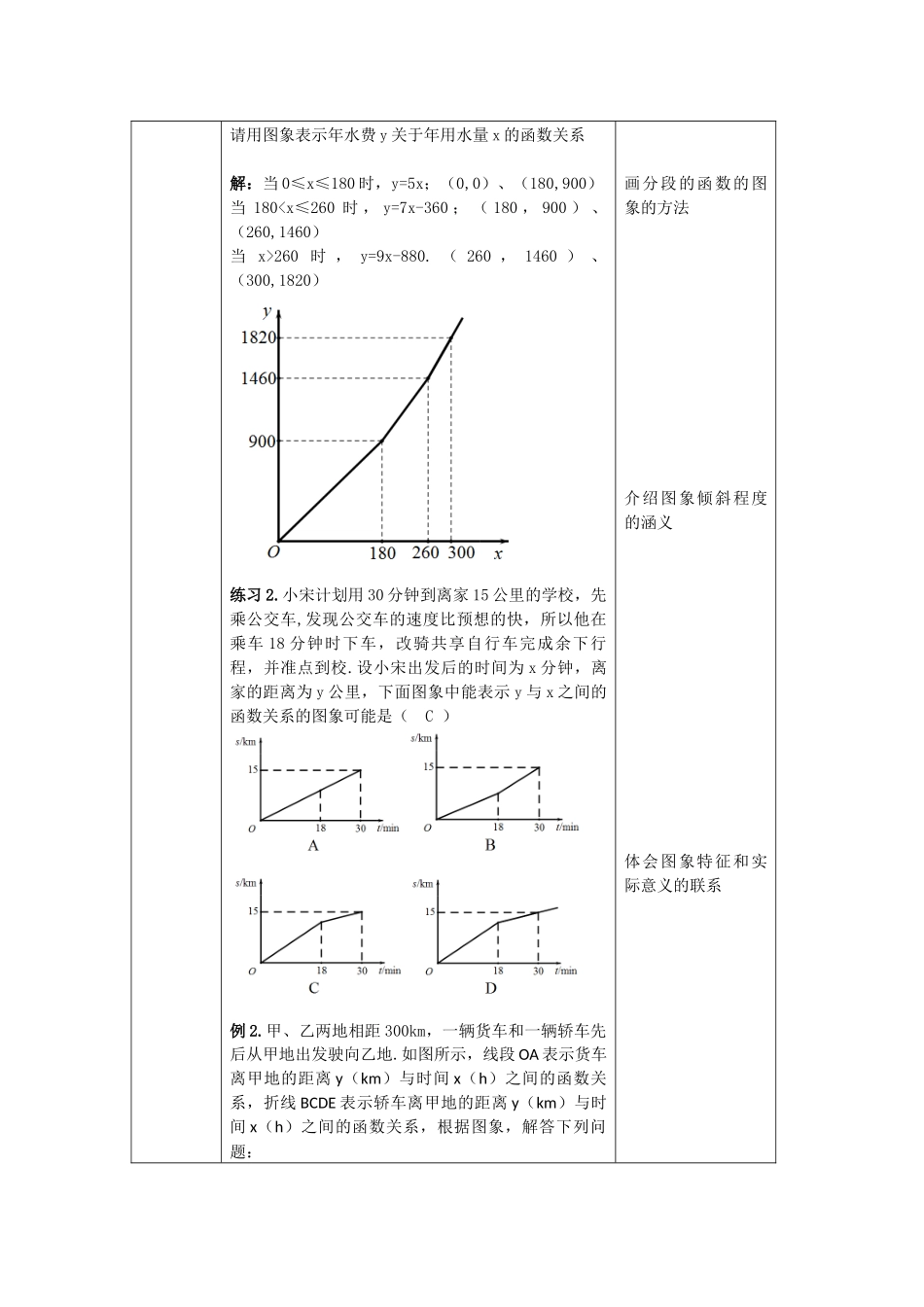
教案教学基本信息课题一次函数的应用(第二课时)学科数学学段:第三学段年级初二教材书名:数学出版社:北京出版社出版日期:2015年1月教学设计参与人员姓名单位设计者霍小宁牛栏山一中实验学校实施者霍小宁牛栏山一中实验学校指导者穆怀如顺义教育研究考试中心课件制作者霍小宁牛栏山一中实验学校其他参与者潘春节牛栏山一中实验学校教学目标及教学重点、难点目标:本节课主要涉及一次函数的概念、图象和性质,通过分析实际问题,建立一次函数(含分段函数)模型,并利用一次函数的有关知识解决实际问题,根据已知的函数图象还原图象所含的信息,尝试解决一些方案选择问题。发展学生的分析能力,识图能力,模型思想,应用意识等。教学重点:与图象有关的一次函数的应用.教学难点:根据图象上的点和图象特征判断实际意义.教学过程(表格描述)教学环节主要教学活动设置意图引入上节课我们以等腰三角形的周长,降价销售,阶梯水价,生产安排等为例解决了以下几个一次函数问题:根据题目条件列出一次函数表达式;根据实际问题的意义确定自变量的取值范围;求给定条件的函数值;求给定条件的函数的最大值等.除了这些内容外,一次函数还有哪些应用呢?事实上一次函数的应用较为广泛,让我们开始今天的学习.介绍本节课的知识背景并引入新课,激发学生的学习兴趣新课例1.甲、乙两个通信公司分别制定了一种移动电话的收费办法.甲公司规定:每月收取月租费50元,每通话一分钟再收费0.4元;乙公司规定:不收取月租费,每通话一分钟收费0.6元.那么,应当怎样选择通信公司才能节省电话费?(通话不到1分钟按1分钟收费)分析:这是一个电话收费问题,涉及到两种收费方通过方程和不等式式.想要选择节省电话费的公司,也就是要比较通话时间相同时两个公司的电话费的大小,然后选择费用少的.我们首先要知道在通话时间相同的情况下两个公司的收费分别是多少.显然,电话费是通话时间的函数.为此可以设通话时间是t分钟,分别列出两家公司的电话费,再进行比较.解:设按照甲、乙两个通信公司的收费标准通话t分钟的话费分别为y1元和y2元,则这两个函数的表达式分别为:y1=0.4t+50(t≥0,t为整数)y2=0.6t(t≥0,t为整数)法一:当y1=y2时,即0.4t+50=0.6t.解得,t=250,当月通话时间为250分钟时,两公司收费相同.当y1>y2时,即0.4t+50>0.6t.解得,t<250,当月通话时间少于250分钟时,应选择乙公司.当y1250,当月通话时间多于250分钟时,...