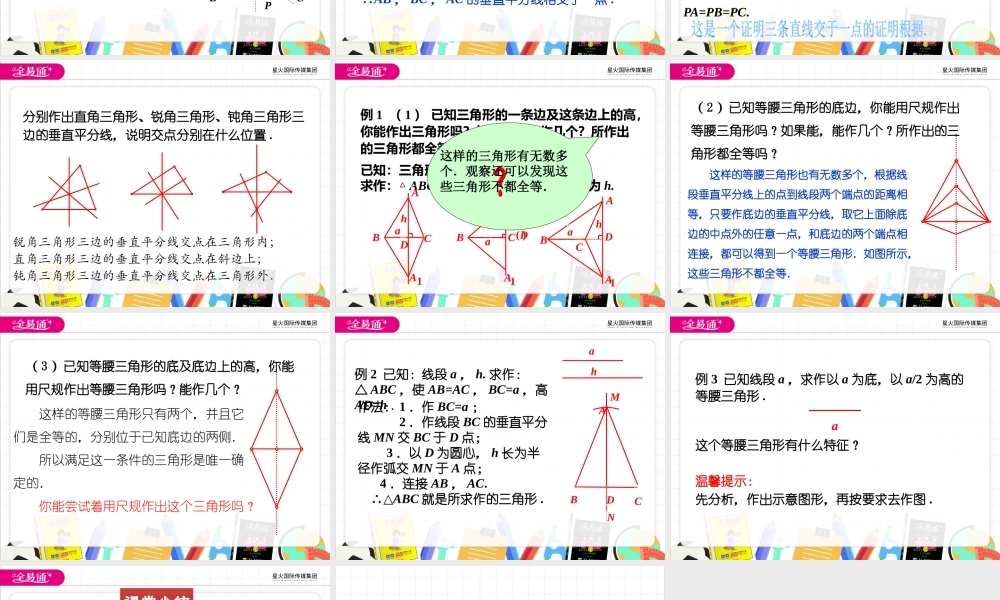
第一章三角形的证明3线段的垂直平分线(第2课时)ABCD1.线段的垂直平分线的性质定理和判断定理.2.线段的垂直平分线的作法.复习旧知利用尺规作三角形三条边的垂直平分线,当作完此题时你发现了什么?发现:三角形三边的垂直平分线交于一点.这一点到三角形三个顶点的距离相等.讲授新课剪一个三角形纸片通过折叠找出每条边的垂直平分线.结论:三角形三条边的垂直平分线相交于一点.怎样证明这个结论呢?点拨:要证明三条直线相交于一点,只要证明其中两条直线的交点在第三条直线上即可.命题:三角形三条边的垂直平分线相交于一点.已知:如图,在△ABC中,AB,BC的垂直平分线相交于点P.求证:点P也在AC的垂直平分线上.ABCP证明:连接AP,BP,CP. 点P在线段AB的垂直平分线上,∴PA=PB.同理,PB=PC.∴PA=PC.∴点P在线段AB的垂直平分线上,∴AB,BC,AC的垂直平分线相交于一点.ABCP定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.如图,在△ABC中, c,a,b分别是AB,BC,AC的垂直平分线(已知),∴c,a,b相交于一点P,且PA=PB=PC.ABCPabc分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.锐角三角形三边的垂直平分线交点在三角形内;直角三角形三边的垂直平分线交点在斜边上;钝角三角形三边的垂直平分线交点在三角形外.例1(1)已知三角形的一条边及这条边上的高,你能作出三角形吗?如果能,能作几个?所作出的三角形都全等吗?已知:三角形的一条边a和这边上的高h.求作:△ABC,使BC=a,BC边上的高为h.1ADCBAah()DCBAah1ADCBAah1A这样的三角形有无数多个.观察还可以发现这些三角形不都全等.(2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗?如果能,能作几个?所作出的三角形都全等吗?这样的等腰三角形也有无数多个,根据线段垂直平分线上的点到线段两个端点的距离相等,只要作底边的垂直平分线,取它上面除底边的中点外的任意一点,和底边的两个端点相连接,都可以得到一个等腰三角形.如图所示,这些三角形不都全等.(3)已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?这样的等腰三角形只有两个,并且它们是全等的,分别位于已知底边的两侧.所以满足这一条件的三角形是唯一确定的.你能尝试着用尺规作出这个三角形吗?例2已知:线段a,h.求作:△ABC,使AB=AC,BC=a,高AD=h.NMDCBahA作法:1.作BC=a;2.作线段BC的垂直平分...