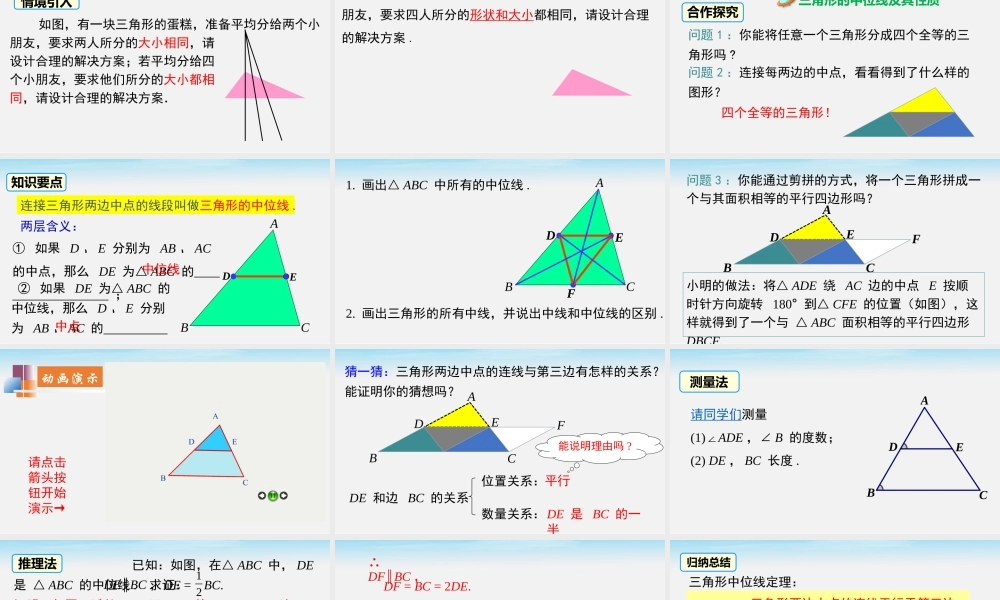
八下数学教学课件(HK)19.2平行四边形第19章四边形第4课时三角形的中位线导入新课如图,有一块三角形的蛋糕,准备平均分给两个小朋友,要求两人所分的大小相同,请设计合理的解决方案;若平均分给四个小朋友,要求他们所分的大小都相同,请设计合理的解决方案.情境引入如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状和大小都相同,请设计合理的解决方案.导入新课问题1:你能将任意一个三角形分成四个全等的三角形吗?合作探究问题2:连接每两边的中点,看看得到了什么样的图形?四个全等的三角形!三角形的中位线及其性质ABCD连接三角形两边中点的线段叫做三角形的中位线.E知识要点两层含义:②如果DE为△ABC的中位线,那么D、E分别为AB、AC的①如果D、E分别为AB、AC的中点,那么DE为△ABC的;中位线中点FDABC1.画出△ABC中所有的中位线.2.画出三角形的所有中线,并说出中线和中位线的区别.E问题3:你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?小明的做法:将△ADE绕AC边的中点E按顺时针方向旋转180°到△CFE的位置(如图),这样就得到了一个与△ABC面积相等的平行四边形DBCFADEFCB动画演示请点击箭头按钮开始演示→猜一猜:三角形两边中点的连线与第三边有怎样的关系?能证明你的猜想吗?ADEFCBDE和边BC的关系数量关系:位置关系:平行DE是BC的一半能说明理由吗?请同学们测量(1)∠ADE,∠B的度数;(2)DE,BC长度.测量法EDBAC已知:如图,在△ABC中,DE是△ABC的中位线.求证:DE∥BC,DE=BC.EABCDF12证明:如图,延长DE至F,使EF=DE,连接CF. AE=CE,∠AED=∠CEF,DE=FE,∴△ADE≌△CFE.∴AD=CF,∠A=∠ECF.∴CF∥AB.推理法 AD=BD,∴四边形DBCF是平行四边形.∴BD=CF.∴DF∥BC,∴DE∥BC,DE=BC.12DF=BC=2DE.EABCDF三角形中位线定理:三角形两边中点的连线平行于第三边,并且等于第三边的一半.用数学语言表示EABCD DE是△ABC的中位线,归纳总结∴DE∥BC,1.2DEBC【定理的理解】(1)从条件看,以后我们看到中点,尤其是两个或者两个以上的中点时,就要联想到三角形的中位线定理;(2)从结论看,它既可以得到线段的位置关系(平行),又可以得到线段的数量关系(倍分关系),大家以后在解决相关问题时要两方面结合起来灵活应用.1.如左图,MN为△ABC的中位线,若∠ABC=61°,则∠AMN=°;若MN=12,则BC长为.AMBCN6124练一练ADBCE2.如右图,△ABC中,D,E分别为AB,AC的中点,当BC=10cm时,则DE=c...