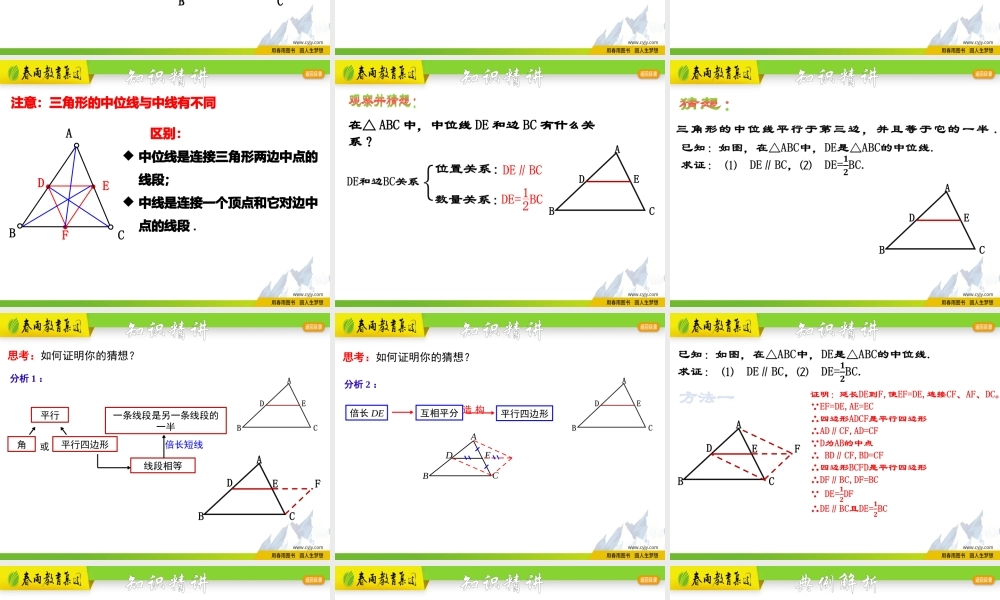
理解三角形中位线的概念,掌握三角形的中位线定理.能利用三角形的中位线定理解决有关证明和计算问题.学习目标ABCDE为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D、E,若测出DE的长,就能求出池塘BC的长.情境引入你知道这是为什么吗?我们一起来探究一下吧!之前我们讲到:平行四边形是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题.知识精讲那我们能不能用平行四边形的知识来解决三角形的问题呢?剪一刀,将一张三角形纸片剪成一张三角形纸片和一张梯形纸片.问题1:如果要求剪得的两张纸片能拼成平行四边形,剪痕的位置有什么要求?ABCDE中点知识精讲问题2:要把所剪得的两个图形拼成一个平行四边形,可将其中的三角形作怎样的图形变换?知识精讲连结三角形两边中点的线段叫三角形的中位线.三角形有三条中位线 D、E分别为AB、AC的中点∴DE为△ABC的中位线同理DF、EF也为△ABC的中位线EDFACB知识精讲EDFACB注意:三角形的中位线与中线有不同区别:中位线是连接三角形两边中点的线段;中线是连接一个顶点和它对边中点的线段.知识精讲在△ABC中,中位线DE和边BC有什么关系?ABCDE知识精讲ABCDE三角形的中位线平行于第三边,并且等于它的一半.知识精讲平行角平行四边形或线段相等一条线段是另一条线段的一半倍长短线分析1:思考:如何证明你的猜想?ABCDEF知识精讲分析2:ABCDE互相平分构造平行四边形倍长DE思考:如何证明你的猜想?知识精讲ABCDEF方法一知识精讲ABCDEF方法二知识精讲三角形的中位线平行且等于第三边的一半.三角形的中位线平行且等于第三边的一半.几何语言: DE是△ABC的中位线(或AD=BD,AE=CE)CEDBA1DE//BC2①证明平行问题②证明一条线段是另一条线段的两倍或一半用途三角形的中位线的性质:知识精讲已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.ABCDEFGH典例解析ABCDEFGH证明:如图,连接AC EF是△ABC的中位线1EF//AC2同理得:1GH//AC2GH//EF∴四边形EFGH是平行四边形①有中点连线而无三角形,要作辅助线产生三角形②有三角形而无中位线,要连结两边中点得中位线典例解析如图:在△ABC中,DE是中位线.(1)若∠ADE=60°,则∠B=度,为什么?(2)若BC=8cm,则DE=cm,为什么?604ABCDE针对练习1.如图2:在△ABC中,D、E、F分别是各边中点AB=6cm,AC=8cm,BC=10cm,则△...