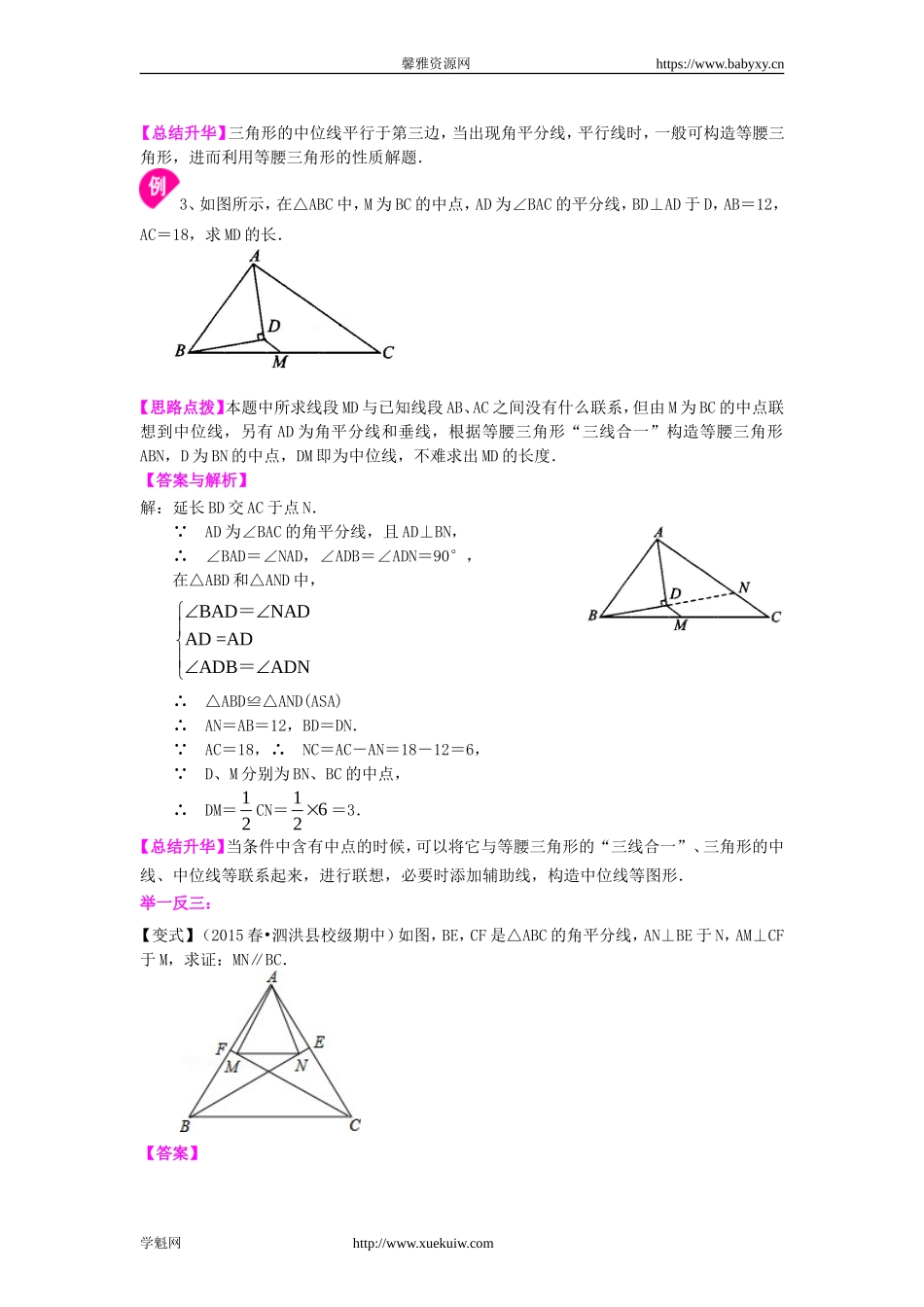
馨雅资源网https://www.babyxy.cn三角形中位线定理责编:杜少波【学习目标】1.理解三角形的中位线的概念,掌握三角形的中位线定理.2.掌握中点四边形的形成规律.【要点梳理】要点一、三角形的中位线1.连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于第三边,并且等于第三边的一半.要点诠释:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的12,每个小三角形的面积为原三角形面积的14.(3)三角形的中位线不同于三角形的中线.要点二、顺次连接任意四边形各边中点得到的四边形的形状顺次连接任意四边形各边中点得到的四边形是平行四边形.【典型例题】类型一、三角形的中位线1、如图,已知P、R分别是长方形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么下列结论成立的是()A.线段EF的长逐渐增大B.线段EF的长逐渐变小C.线段EF的长不变D.无法确定【答案】C;【解析】连AR,由E、F分别为PA,PR的中点知EF为△PAR的中位线,则12EFAR,而AR长不变,故EF大小不变.【总结升华】当条件中含有中点的时候,要将它与中位线联系起来,进行联想,必要时添加辅助线,构造中位线图形.举一反三:【变式】(2015秋•青岛校级月考)在△ABC中,中线BE、CF交于点O,M、N分别是BO、CO中点,则四边形MNEF是什么特殊四边形?并说明理由.学魁网http://www.xuekuiw.com馨雅资源网https://www.babyxy.cn【答案】5;解:四边形MNEF是平行四边形.理由如下: BE、CF是中线,∴E、F分别是AC、AB的中点,∴EF是△ABC的中位线,∴EF∥BC且EF=BC, M、N分别是BO、CO中点,∴MN是△OBC的中位线,∴MN∥BC且MN=BC,∴EF∥MN且EF=MN,∴四边形MNEF是平行四边形.2、如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是()A.2B.3C.52D.4【思路点拨】利用中位线定理,得到DE∥AB,根据平行线的性质,可得∠EDC=∠ABC,再利用角平分线的性质和三角形内角外角的关系,得到DF=DB,进而求出DF的长.【答案解析】解:在△ABC中,D、E分别是BC、AC的中点∴DE∥AB∴∠EDC=∠ABC BF平分∠ABC∴∠EDC=2∠FBD在△BDF中,∠EDC=∠FBD+∠BFD∴∠DBF=∠DFB∴FD=BD=12BC=12×6=3.学魁网http://www.xuekuiw.com馨雅资源网https://www.babyxy.cn...