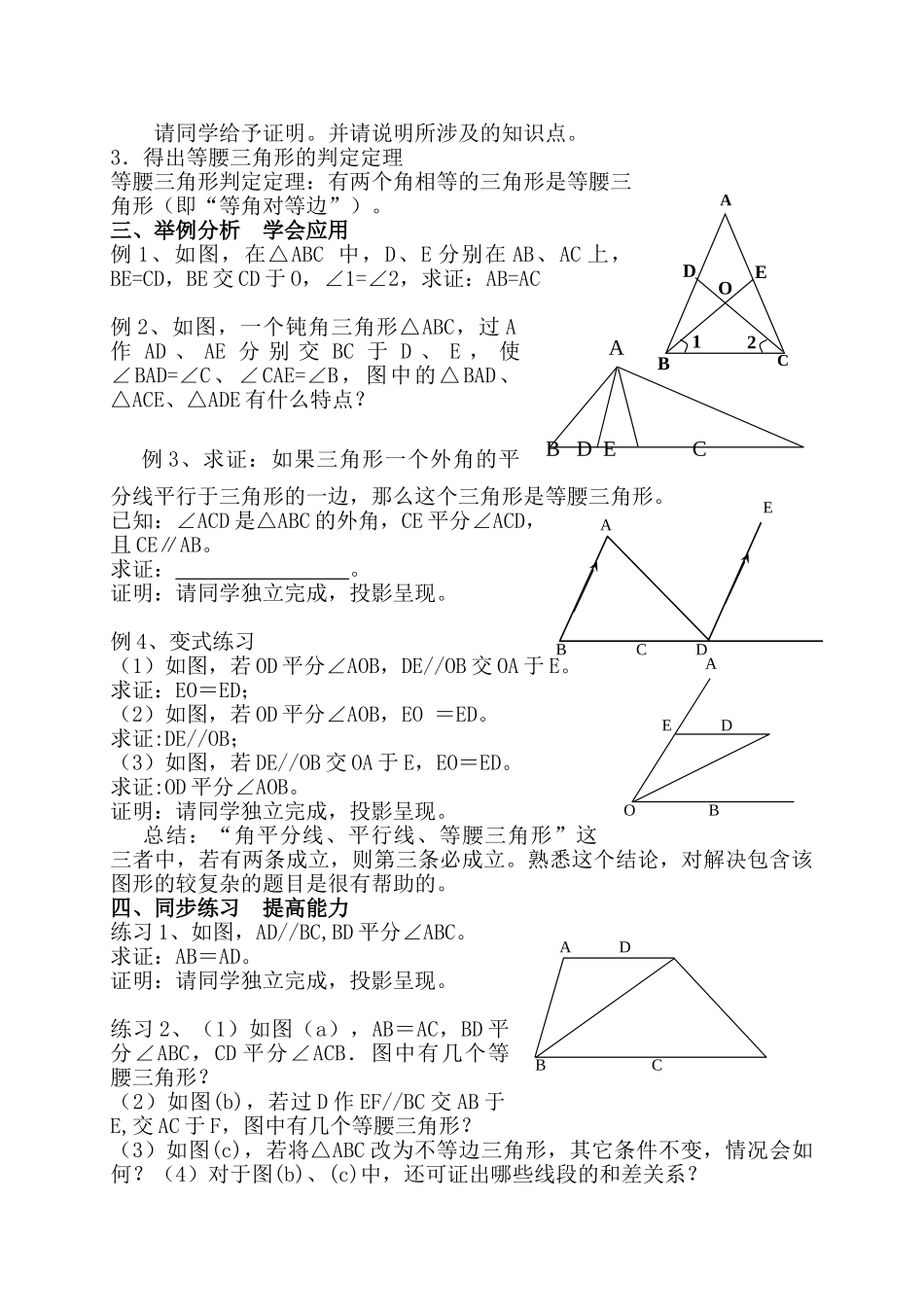
课题:等腰三角形的判定教学目标1.在探究的基础上提出如何确定一个三角形是等腰三角形;2.回顾“互逆命题”关系,提出等腰三角形判定,同时提高逆向思维能力;3.通过对等腰三角形判定定理的证明,提高学生的逻辑证明能力;4.通过例3、4的教学,使学生认识角平分线、平行线与等腰三角形的内在规律。并由此提高学生综合应用能力。重点难点1.重点:等腰三角形判定定理的提出、证明与应用;2.难点:等腰三角形判定定理的证明,性质与判定的区别。教学过程一、实践探究提出问题1.某班进行野外郊游,老师要求同学们测量P、Q两点间距离,但P、Q两点被一个水池隔开了,手上没有测量工具可以直接测量P、Q间距离。一位聪明的学生利用所学几何知识解决了这个问题。他从同学的书包内找到了两把圆规,当成简易“测角仪”,并先在水池的一侧空地上找了一个点A,连结AP并延长到B,使∠APQ=2∠ABQ,然后步量出BP的长度。这个长度就是PQ的距离。你认为这种方法正确吗?问题1:从条件∠APQ=2∠ABQ,我们能够得到什么结果?问题2:由∠PQB=∠PBQ能够得到PQ=PB吗?为什么?2.如图,将长方形沿对角线折起抹平,点C落在了点C1处,则重叠的三角形△BDE是等腰三角形。为什么?二、逆向思考提出“判定”1.逆命题命题的结构:如果……,那么……。即:题设,结论。逆命题:原命题的结论当题设,原命题的题设当结论。请写出“等腰三角形的两底角相等”的逆命题。总结:逆命题可以有以下几种叙述方法:①如果一个三角形的两个内角相等,那么这个三角形是等腰三角形;②如果一个三角形的两个内角相等,那么这个三角形有两条边相等;③如果一个三角形的两个内角相等,那么这两个内角所对的边也相等即“等角对等边”。也可简单地叙述为:有两个角相等的三角形是等腰三角形。注意:不可说“两底角相等”,为什么?2.将命题“有两个角相等的三角形是等腰三角形”翻译成几何语言,并写出“已知、求证”。已知:如图,△ABC中,∠B=∠C。求证:AB=AC。BCAABPQ3ABCDEC1请同学给予证明。并请说明所涉及的知识点。3.得出等腰三角形的判定定理等腰三角形判定定理:有两个角相等的三角形是等腰三角形(即“等角对等边”)。三、举例分析学会应用例1、如图,在△ABC中,D、E分别在AB、AC上,BE=CD,BE交CD于O,∠1=∠2,求证:AB=AC例2、如图,一个钝角三角形△ABC,过A作AD、AE分别交BC于D、E,使∠BAD=∠C、∠CAE=∠B,图中的△BAD、△ACE、△ADE有什么特点?例3、求证:如果...