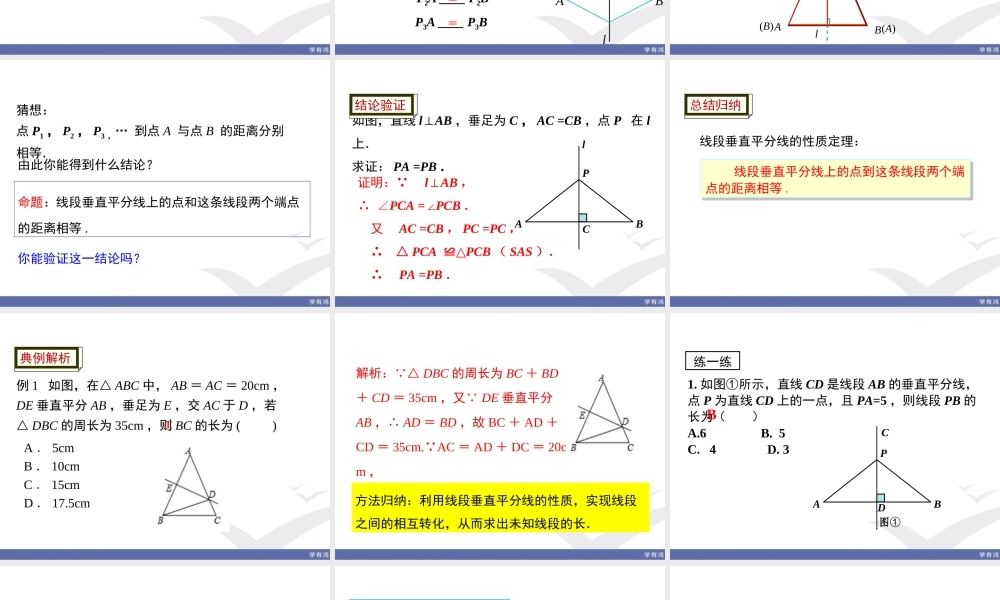
1.3线段的垂直平分线第1课时线段的垂直平分线【学习目标】1.会用学过的公理和定理证明线段的垂直平分线的性质、判定定理.2.能够利用尺规做已知线段的垂直平分线.【学习重点】线段的垂直平分线的性质、判定定理的证明.【学习难点】尺规做已知线段的垂直平分线.教学目标某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?ABC新课引入观察:已知点A与点A′关于直线l对称,如果线段AA′沿直线l折叠,则点A与点A′重合,AD=A′D,∠1=2=90°∠,即直线l既平分线段AA′,又垂直线段AA′.●●lAA′D21(A)线段垂直平分线的性质我们把垂直且平分一条线段的直线叫作这条线段的垂直平分线.由上可知:线段是轴对称图形,线段的垂直平分线是它的对称轴.总结归纳如图,直线l垂直平分线段AB,P1,P2,P3,…是l上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么?请猜想点P1,P2,P3,…到点A与点B的距离之间的数量关系.ABlP1P2P3P1A____P1BP2A____P2BP3A____P3B===新课探究作关于直线l的轴反射(即沿直线l对折),由于l是线段AB的垂直平分线,因此点A与点B重合.从而线段PA与线段PB重合,于是PA=PB.(A)(B)BAPl新课探究猜想:点P1,P2,P3,…到点A与点B的距离分别相等.命题:线段垂直平分线上的点和这条线段两个端点的距离相等.由此你能得到什么结论?你能验证这一结论吗?如图,直线l⊥AB,垂足为C,AC=CB,点P在l上.求证:PA=PB.证明: l⊥AB,∴∠PCA=∠PCB.又AC=CB,PC=PC,∴△PCA≌△PCB(SAS).∴PA=PB.PABlC结论验证线段垂直平分线上的点到这条线段两个端点的距离相等.线段垂直平分线上的点到这条线段两个端点的距离相等.线段垂直平分线的性质定理:总结归纳例1如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为()A.5cmB.10cmC.15cmD.17.5cmC典例解析解析: △DBC的周长为BC+BD+CD=35cm,又 DE垂直平分AB,∴AD=BD,故BC+AD+CD=35cm.AC =AD+DC=20cm,∴BC=35-20=15(cm).故选C.方法归纳:利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为()A.6B.5C.4D.3BPABCD图①练一练2.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边...