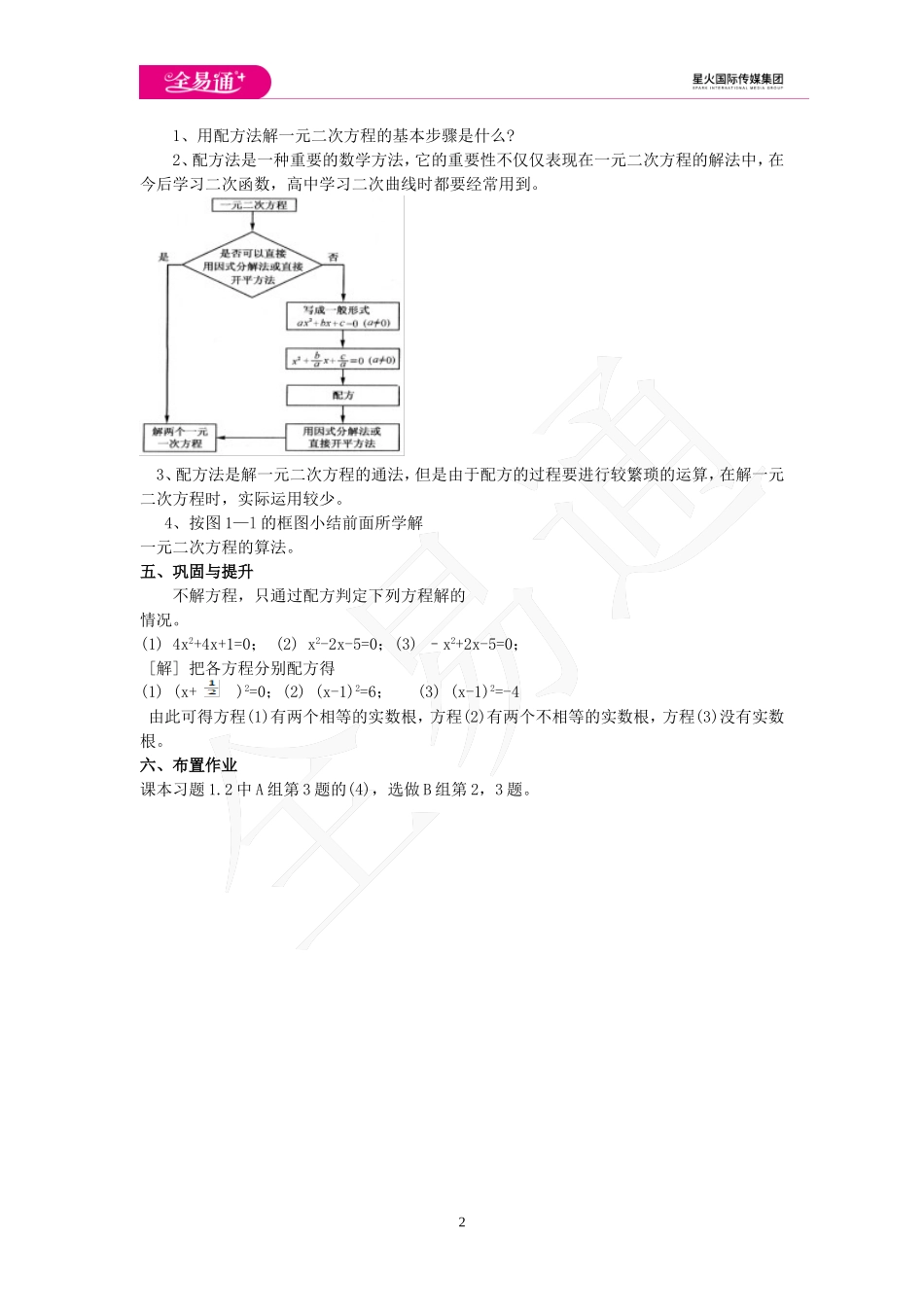
12.2一元二次方程的解法第3课时教学目标【知识与能力】1、理解用配方法解一元二次方程的基本步骤。2、会用配方法解二次项系数不为1的一元二次方程。3、进一步体会化归的思想方法。【过程与方法】经历将二次项系数不为“1”的一元二次方程化为二次项系数为“1”的一元二次方程的过程,让学生体会化归思想。【情感态度价值观】通过分组讨论与合作交流,让学生体验到学习的乐趣。同时同过对复杂问题的抽象化归,使问题简单化,培养学生的自信心。教学重难点【教学重点】用配方法解二次项系数不为1的一元二次方程。【教学难点】如何配方。课前准备无教学过程一、预学1、用配方法解方程x2+x-1=0,学生练习后再完成课本P.13的“做一做”.2、用配方法解二次项系数为1的一元二次方程的基本步骤是什么?二、探究现在我们已经会用配方法解二次项系数为1的一元二次方程,而对于二次项系数不为1的一元二次方程能不能用配方法解?怎样解这类方程:2x2-4x-6=0让学生议一议解方程2x2-4x-6=0的方法,然后总结得出:对于二次项系数不为1的一元二次方程,可将方程两边同除以二次项的系数,把二次项系数化为1,然后按上一节课所学的方法来解。让学生进一步体会化归的思想。三、精讲1、展示课本P.14例8,按课本方式讲解。2、引导学生完成课本P.14例9的填空。3、归纳用配方法解一元二次方程的基本步骤:首先将方程化为二次项系数是1的一般形式;其次加上一次项系数的一半的平方,再减去这个数,使得含未知数的项在一个完全平方式里;最后将配方后的一元二次方程用因式分解法或直接开平方法来解。四、课堂小结21、用配方法解一元二次方程的基本步骤是什么?2、配方法是一种重要的数学方法,它的重要性不仅仅表现在一元二次方程的解法中,在今后学习二次函数,高中学习二次曲线时都要经常用到。3、配方法是解一元二次方程的通法,但是由于配方的过程要进行较繁琐的运算,在解一元二次方程时,实际运用较少。4、按图1—l的框图小结前面所学解一元二次方程的算法。五、巩固与提升不解方程,只通过配方判定下列方程解的情况。(1)4x2+4x+1=0;(2)x2-2x-5=0;(3)–x2+2x-5=0;[解]把各方程分别配方得(1)(x+)2=0;(2)(x-1)2=6;(3)(x-1)2=-4由此可得方程(1)有两个相等的实数根,方程(2)有两个不相等的实数根,方程(3)没有实数根。六、布置作业课本习题1.2中A组第3题的(4),选做B组第2,3题。