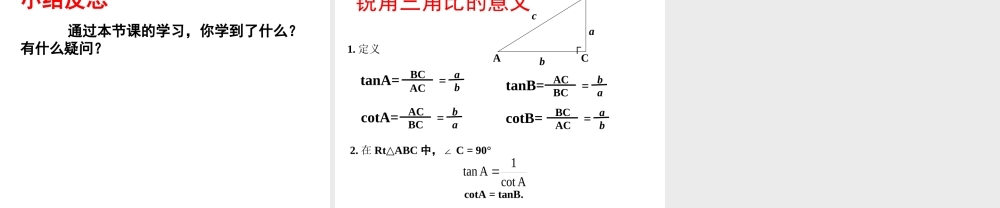
25.1(1)锐角的三角比的意义角的关系:直角三角形两锐角互余.直角三角形边的关系:两条直角边的平方和等于斜边的平方(勾股定理).边与角的关系(特殊的直角三角形中):含30°角的直角三角形;含45°角的直角三角形.对于一个直角三角形,如果给定了它的一个锐角的大小,那么它的两条直角边的比值是否是一个确定的值?结论1如果给定直角三角形的一个锐角,那么这个锐角的对边与邻边的长度的比值就是一个确定的数.一个确定的值的邻边锐角的对边锐角AA问题1当直角三角形中一个锐角的大小变化时,这个锐角的对边与邻边的长度的比值随着变化吗?结论2直角三角形中,一个锐角的对边与邻边的长度的比值随着这个锐角的大小的变化而变化.问题2结论2:直角三角形中,一个锐角的对边与邻边的长度的比值随着这个锐角的大小的变化而变化.结论1:如果给定直角三角形的一个锐角,那么这个锐角的对边与邻边的长度的比值就是一个确定的数.正切:直角三角形中一个锐角的对边与邻边的比,锐角A的正切,记作tanAbaAAA的邻边锐角的对边锐角tanabAAA的对边锐角的邻边锐角cot当直角三角形的一个锐角的大小确定时,这个锐角的邻边与对边的比值也是确定的.余切:直角三角形中一个锐角的邻边与对边的比,锐角A的正切,记作cotA1.在直角三角形中定义,∠A是锐角;2.tanA、cotA的值只与∠A的大小有关,而与直角三角形的边长无关;3.tanA、cotA是一个比值,无单位注意1.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为点D.(1)tanA可以用什么表示?(2)tanB呢(3)tan∠ACD呢?DCBA练习一2.在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值()A.扩大100倍B.缩小100倍C.不变D.不能确定C9032tantanABCCACBCAB在中,,,,求和的值.例13232tantanABBCACkBCkCCDABDACDBCD12变式,变式,变式3过点作于点,求和在Rt△ABC中,∠C=90°,正切和余切有怎样的关系?思考1.901213cotRtABCCBCABAB在中,,,,求tan和值.2.在Rt△ABC中,∠B=900,AB=15,tanA=0.6求BC的长.练习二3.在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,且AC=5,CD=4,求tanB.在等腰△ABC中,AB=AC=13,BC=10,求tanB思考通过本节课的学习,你学到了什么?有什么疑问?小结反思ab锐角三角比的意义tanA=ABCab┌cBCAC=bacotA=ACBC=batanB=ACBC=abcotB=BCAC=2.在RtABC△中,∠C=90°cotA=tanB.1.定义1tanAcotA