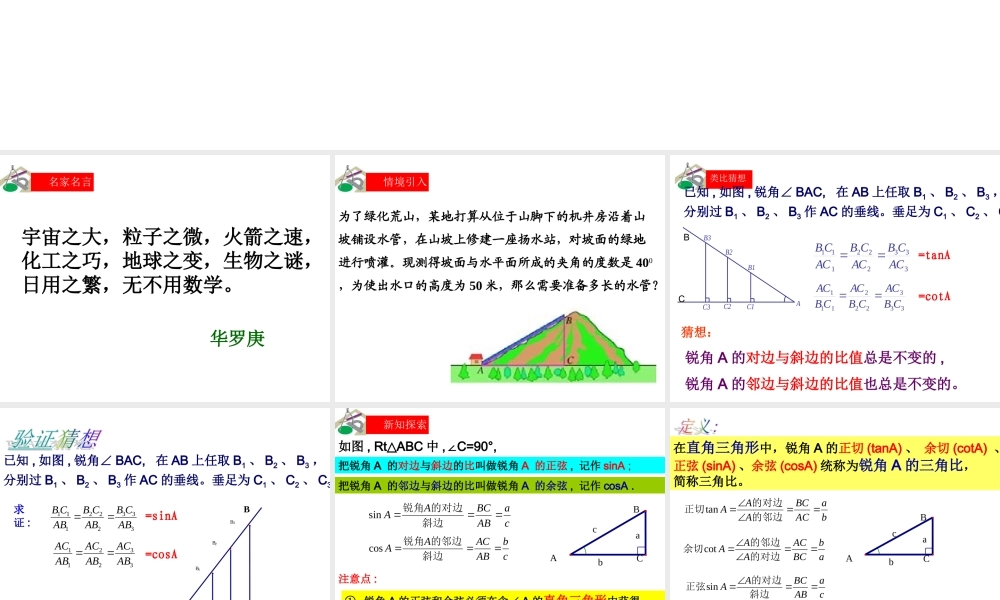
25.1(2)锐角三角比的意义宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无不用数学。华罗庚情境引入名家名言为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌。现测得坡面与水平面所成的夹角的度数是400,为使出水口的高度为50米,那么需要准备多长的水管?情境引入类比猜想C3C2C1AB1B2B3333222111ACCBACCBACCB已知,如图,锐角∠BAC,在AB上任取B1、B2、B3,分别过B1、B2、B3作AC的垂线。垂足为C1、C2、CBC=tanA333222111CBACCBACCBAC=cotA猜想:锐角A的对边与斜边的比值总是不变的,锐角A的邻边与斜边的比值也总是不变的。已知,如图,锐角∠BAC,在AB上任取B1、B2、B3,分别过B1、B2、B3作AC的垂线。垂足为C1、C2、C3CBB3B2B1AC1C3C2求证:333222111ABCBABCBABCB332211ABACABACABAC△AB1C1∽△AB2C2∽△AB3C3=sinA=cosA如图,RtABC△中,C=90°,∠把锐角A的对边与斜边的比叫做锐角A的正弦,记作sinA;把锐角A的邻边与斜边的比叫做锐角A的余弦,记作cosA.注意点:①锐角A的正弦和余弦必须在含∠A的直角三角形中获得。②sinA是表示锐角A的正弦,它是一个整体,单独的sin无意义。bacACBcaABBCAA斜边的对边锐角sincbABACAA斜边的邻边锐角cos新知探索在直角三角形中,锐角A的正切(tanA)、余切(cotA)、正弦(sinA)、余弦(cosA)统称为锐角A的三角比,简称三角比。bacACBbaACBCAAA的邻边的对边正切tanabBCACAAA的对边的邻边余切cotcaABBCAA斜边的对边正弦sincbABACAA斜边的邻边余弦cos理解记忆邻座的两个同学一个说三角比,另一说出是哪两条线段的比。bacACBbacACB问题拓展1、各个三角比的取值范围分别是什么?tanA>0cotA>00