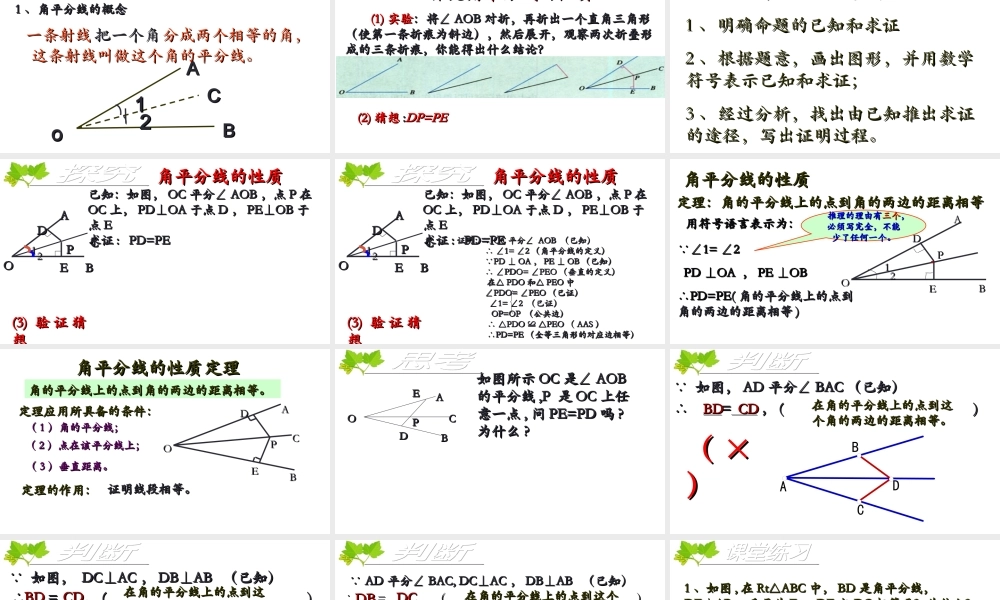
角平分线的性质角平分线的性质11、角平分线的概念、角平分线的概念一条射线一条射线把一个角把一个角分成两个相等的角,分成两个相等的角,这条射线叫做这个角的平分线。这条射线叫做这个角的平分线。ooBBCCAA1122探究角平分线的性质探究角平分线的性质(1)(1)实验实验:将∠:将∠AOBAOB对折,再折出一个直角三角形对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?成的三条折痕,你能得出什么结论?(2)(2)猜想猜想::DP=PEDP=PE证明几何命题的一般步骤:证明几何命题的一般步骤:11、明确命题的已知和求证、明确命题的已知和求证22、根据题意,画出图形,并用数学、根据题意,画出图形,并用数学符号表示已知和求证;符号表示已知和求证;33、经过分析,找出由已知推出求证、经过分析,找出由已知推出求证的途径,写出证明过程。的途径,写出证明过程。PPAAOOBBCCEEDD1122已知:如图,已知:如图,OCOC平分∠平分∠AOBAOB,点,点PP在在OCOC上,上,PD⊥OAPD⊥OA于点于点DD,,PE⊥OBPE⊥OB于于点点EE求证求证:PD=PE:PD=PE角平分线的性质角平分线的性质(3)(3)验证猜验证猜想想证明: 证明: OCOC平分∠平分∠AOBAOB(已知)(已知)∴∠∴∠1=∠21=∠2(角平分线的定义)(角平分线的定义) PD⊥OAPD⊥OA,,PE⊥OBPE⊥OB(已知)(已知)∴∠∴∠PDO=∠PEOPDO=∠PEO(垂直的定义)(垂直的定义)在△在△PDOPDO和△和△PEOPEO中中∠∠PDO=∠PEOPDO=∠PEO(已证)(已证)∠∠1=∠21=∠2(已证)(已证)OP=OPOP=OP(公共边)(公共边)∴∴△△PDO≌△PEOPDO≌△PEO((AASAAS))∴∴PD=PEPD=PE(全等三角形的对应边相等)(全等三角形的对应边相等)PPAAOOBBCCEEDD1122已知:如图,已知:如图,OCOC平分∠平分∠AOBAOB,点,点PP在在OCOC上,上,PD⊥OAPD⊥OA于点于点DD,,PE⊥OBPE⊥OB于于点点EE求证求证:PD=PE:PD=PE角平分线的性质角平分线的性质(3)(3)验证猜验证猜想想角平分线的性质角平分线的性质定理:角的平分线上的点到角的两边的距离相等定理:角的平分线上的点到角的两边的距离相等用符号语言表示为:用符号语言表示为:AAOOBBPPEEDD1122 ∠ ∠1=∠21=∠2PD⊥OAPD⊥OA,,PE⊥OBPE⊥OB∴∴PD=PEPD=PE((角的平分线上的点到角的平分线上的点到角的两边的距离相等角的两边的距离相等))推理的理由有推理的理由有三...