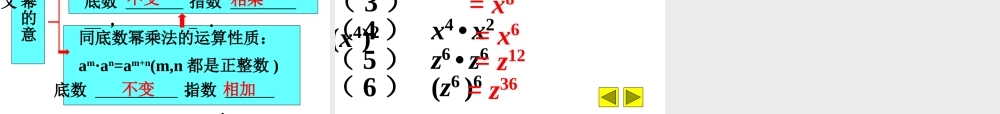课前练习1.计算:(1)(-2)3•(-2)2(2)(-2)4•22(3)22•(-2)5(4)(-b)4•(-b)3(5)-a6•(-a)3(6)-a3•(-a4)=(-2)5=26=(-2)7=a9=a7=(-b)7=-25=-b7=-27同底数幂的乘法1、指出下列各幂的底数和指数:(a4)3;(23)4;(a3)5;23a4a33)4的底数是,指数是2342的3次幂的4次方课前练习2.指出下列各幂的底数和指数:(a4)3;(23)4;(a3)5;23a4a34)3的底数是,指数是a43a的4次幂的3次方3.指出下列各幂的底数和指数:(a4)3;(23)4;(a3)5;23a4a33)5的底数是,指数是a35a的3次幂的5次方学习目标:1、经历探究幂的乘方的运算性质的过程。2、掌握幂的乘方的运算公式并会熟练应用。1、P21【探究】将空格补充完整2、幂的乘方法公式及推导过程熟记公式,理解推导过程,能讲解3、P22例2能利用公式独立完成的将例题做到本子上,不能独立完成的自己看书理解,尽最大努力学会,不理解的做好标记4、P23练习通过学习争取独立完成在本上阅读课本P21----P22解答下列问题自主学习:自学检测:(a4)3(23)4(a3)5探究:=23×23×23×23=a4×a4×a4=a3×a3×a3×a3×a3=a15=212=a12(a4)3=a12;由(23)4=212;(a3)5=a15,(32)3(x7)2(t4)4(y4)236x14y8t16从左到右的变化,请马上回答下列各题的结果:(am)n=(m,n都是正整数)amn请用语言叙述幂的乘方的法则:幂的乘方,______不变,指数。底数相乘用字母简明地表示:(其中m,n都是正整数)(am)n=a()mnn()个=am•am•am••am…n=a(m+m+m++m)()个…(乘方的意义)(同底数幂的乘法)(乘法的定义)(1)(103)5(2)(x4)4(3)(xm)2(4)-(a4)3例1:(1)(103)3(2)(x3)2(3)-(xm)5(4)(a2)3•a5练习:(2)-(y3)3(1)(105)2当堂训练:(3)[(-3)2]3(4)(-32)5=10(5×2)=-y(3×3)=(-3)(2×3)=-(32)5=-310=1010=-y9=(-3)6=36(5)a3•a5+(a2)4(6)(-x2)•(-x4)+(x2)3(7)(a3•a2)2(8)(a3)4+a3•a4(1)(x2)3•(x3)4(2)-y2•(-y)3•[(-y)2]3(3)[(a+b)2]3(4)(x+y)3•[(x+y)2]2(5)[(a-b)•(b-a)2]4。能力提升的值则求已知mmxx2,4注:幂的乘方公式还可逆用.amn=(am)n=(an)m..5,323的值求已知:nmnmaaa解:∵am=3,an=5∴a3m+2n=a3m·a2n=(am)3·(an)2=33×52=675.139.xx解方程:小结同底数幂乘法的运算性质:am·an=am+n(m,n都是正整数)底数,指数.幂的乘方的运算性质:(am)n=amn(m,n都是正整数).底数,指数.相加相乘不变不变幂的意义练习1.计算:(1)(104)3(2)104×103(3)(x4)2(4)x4•x2(5)z6•z6(6)(z6)6=1012=107=x8=x6=z12=z36