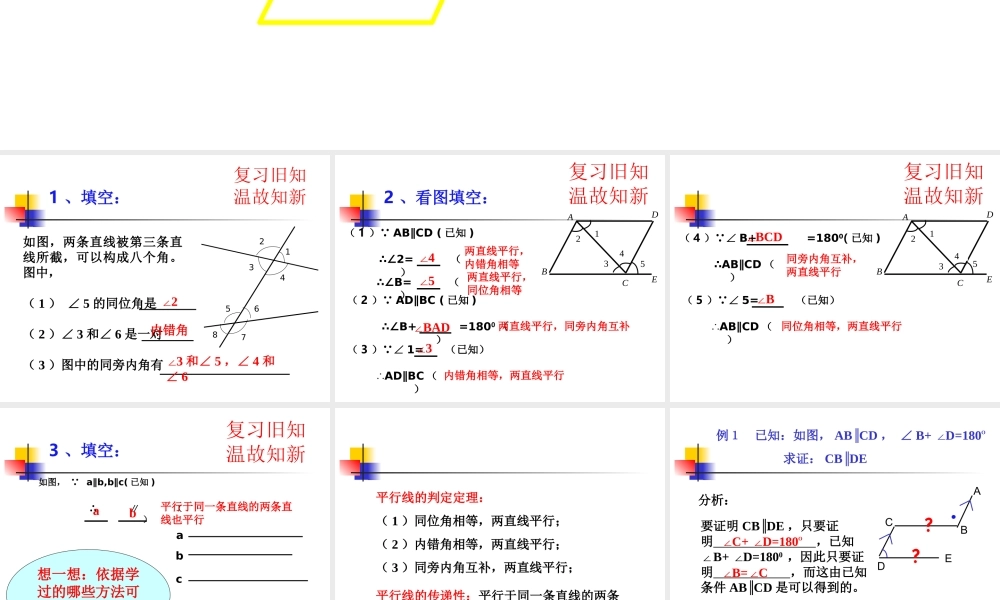
19.2证明举例(1)——有关两直线平行……复习旧知温故知新12345678如图,两条直线被第三条直线所截,可以构成八个角。图中,(1)∠5的同位角是(2)∠3和∠6是一对(3)图中的同旁内角有1、填空:内错角∠2∠3和∠5,∠4和∠6复习旧知温故知新2、看图填空:(1) AB∥CD(已知)∴∠2=()BCADE14532∴∠B=()(2) AD∥BC(已知)∴∠B+=1800()(3) ∠1=(已知)∴AD∥BC()∠4两直线平行,内错角相等∠5两直线平行,同位角相等∠BAD两直线平行,同旁内角互补∠3内错角相等,两直线平行复习旧知温故知新(4) ∠B+=1800(已知)∴AB∥CD()BCADE14532(5) ∠5=(已知)∴AB∥CD()∠BCD同旁内角互补,两直线平行∠B同位角相等,两直线平行复习旧知温故知新如图, a∥b,b∥c(已知)∴∥()3、填空:abc想一想:依据学过的哪些方法可以证明两条直线平行?ab平行于同一条直线的两条直线也平行平行线的判定定理:(1)同位角相等,两直线平行;(2)内错角相等,两直线平行;(3)同旁内角互补,两直线平行;平行线的传递性:平行于同一条直线的两条直线也平行例1已知:如图,ABCD∥,∠B+D=180∠O求证:CBDE∥ABCDE分析:要证明CBDE∥,只要证明,已知∠B+D=180∠0,因此只要证明,而这由已知条件ABCD∥是可以得到的。∠C+D=180∠O∠B=C∠.﹖﹖例1变式练习:已知:如图,CBDE∥,∠B+D=180∠O求证:ABCD∥ABCDE要证明ABCD∥,只要证明,已知∠B+D=180∠0,因此只要证明,而这由已知条件CBDE∥是可以得到的。分析:﹖﹖.∠B=C∠∠C+D=180∠O例2已知:如图,点D,E,F分别是AC、AB、BC上的点,DFAB∥,∠DFE=A∠求证:EFAC∥ABCEDF要证明EFAC,∥只要证明又已知∠DFE=A∠,因此只要证明,而这由已知条件DFAB∥得到的。分析:﹖﹖∠A=BEF∠∠DFE=BEF∠例2已知:如图,点D,E,F分别是AC、AB、BC上的点,DFAB∥,∠DFE=A∠求证:EFAC∥ABCEDF要证明EFAC,∥只要证明又已知∠DFE=A∠,因此只要证明,而这由已知条件DFAB∥得到的。分析:﹖﹖∠DFE=FDC∠∠A=FDC∠例2已知:如图,点D,E,F分别是AC、AB、BC上的点,DFAB∥,∠DFE=A∠求证:EFAC∥ABCEDF要证明EFAC,∥只要证明又已知∠DFE=A∠,因此只要证明,而这由已知条件DFAB∥得到的。分析:﹖﹖∠A+AEF=180∠0∠DFE+AEF=180∠0例2变式练习:已知:如图,DFAB∥,EFAC∥求证:∠DFE=A∠ABCEDF﹖﹖练习1已知:如图,∠1=B,2=D∠∠∠求证:ABCD∥CFDEBA12练习2已知:如图,∠C=1,B=D∠∠∠求...