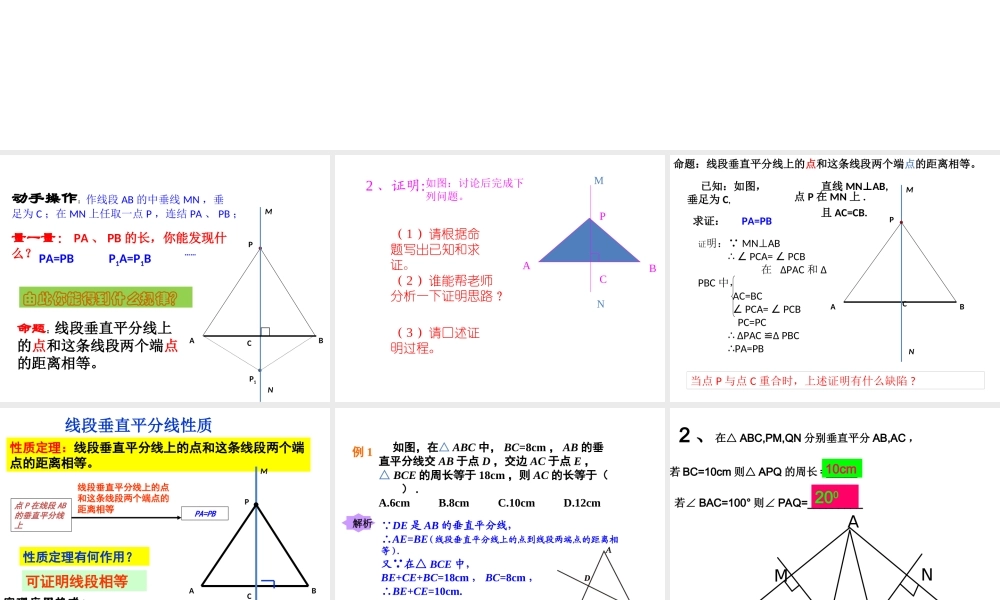
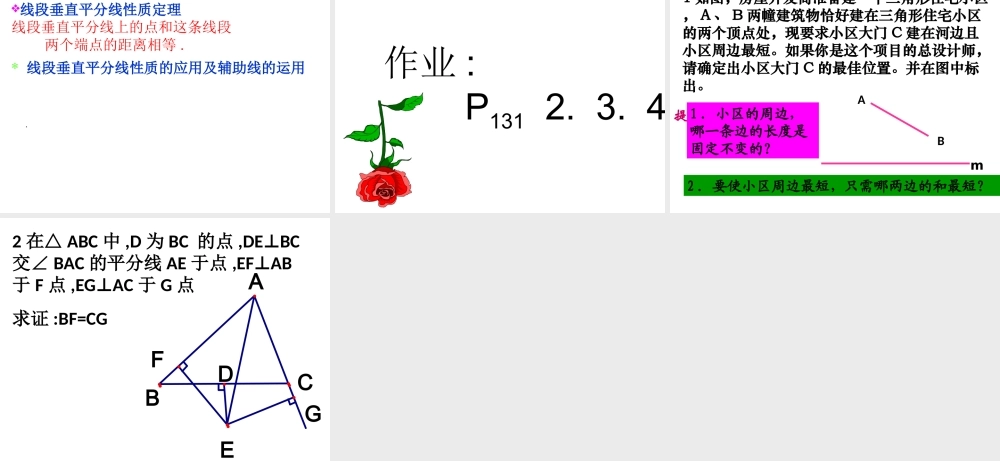
线段的垂直平分线性质ABPA=PBP1P1A=P1B……命题:线段垂直平分线上的点和这条线段两个端点的距离相等。PMNC动手操作:作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?由此你能得到什么规律?2、证明:MNABPC如图:讨论后完成下列问题。(1)请根据命题写出已知和求证。(2)谁能帮老师分析一下证明思路?(3)请口述证明过程。命题:线段垂直平分线上的点和这条线段两个端点的距离相等。ABPMN当点P与点C重合时,上述证明有什么缺陷?CPA=PB直线MNAB,⊥垂足为C,且AC=CB.已知:如图,点P在MN上.求证:证明: MNAB⊥∴∠PCA=PCB∠在ΔPAC和ΔPBC中,AC=BC∠PCA=PCB∠PC=PC∴ΔPACΔPBC≌∴PA=PB性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。ABPMNCPA=PB点P在线段AB的垂直平分线上线段垂直平分线上的点和这条线段两个端点的距离相等性质定理有何作用?可证明线段相等定理应用格式: AC=BC,MN⊥AB,P是MN上任意一点(已知),∴PA=PB(线段垂直平分线上的点与这条线段两个端点距离相等).线段垂直平分线性质如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于().A.6cmB.8cmC.10cmD.12cm例1解析 DE是AB的垂直平分线,∴AE=BE(线段垂直平分线上的点到线段两端点的距离相等).又 在△BCE中,BE+CE+BC=18cm,BC=8cm,∴BE+CE=10cm.∴AC=AE+CE=BE+CE=10cm.故应选择C.2、在△ABC,PM,QN分别垂直平分AB,AC,若BC=10cm则△APQ的周长=_____若∠BAC=100°则∠PAQ=_________QNMCBPA10cm200例2已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.求证:PA=PB=PC;BACMNM’N’PPA=PB=PCPB=PC点P在线段BC的垂直平分线上PA=PB点P在线段AB的垂直平分线上分析:例2已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.求证:PA=PB=PC;证明: 点P在线段AB的垂直平分线MN上,∴PA=PB(?).同理PB=PC.∴PA=PB=PC.BACMNM’N’P变式题:如图所示,直线MN和DE分别是线段AB、BC的垂直平分线,它们交于点O,试判断线段OA和OC是否相等?请说明理由?NMOEDCBA解:相等,连接OB. MN是线段AB的垂直平分线(已知)∴OA=OB(线段中垂线的性质)又 DE是线段BC的垂直平分线(已知)∴OB=OC(线段中垂线的性质)∴OA=OC(等量代换)张店区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区...