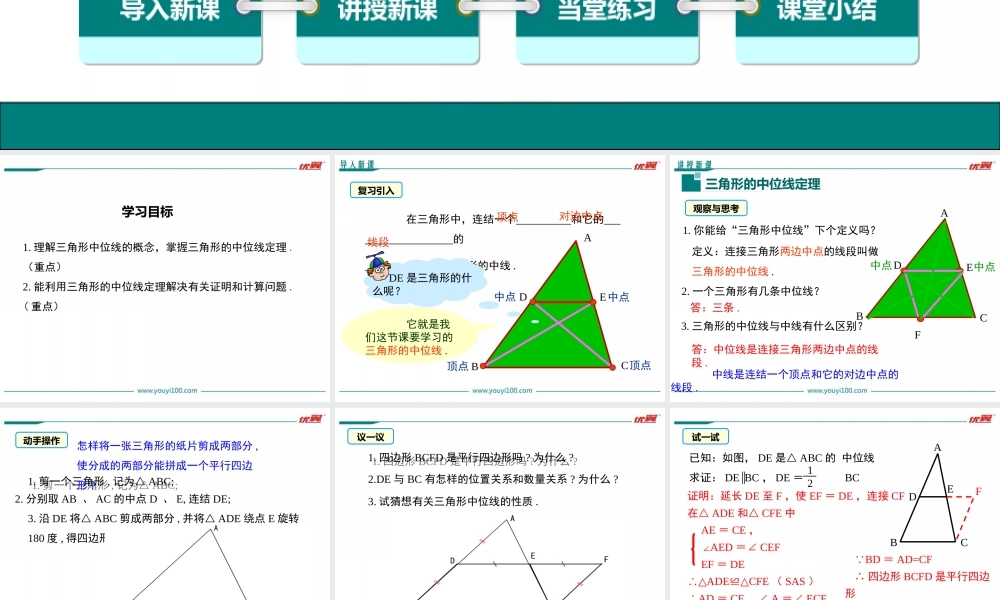
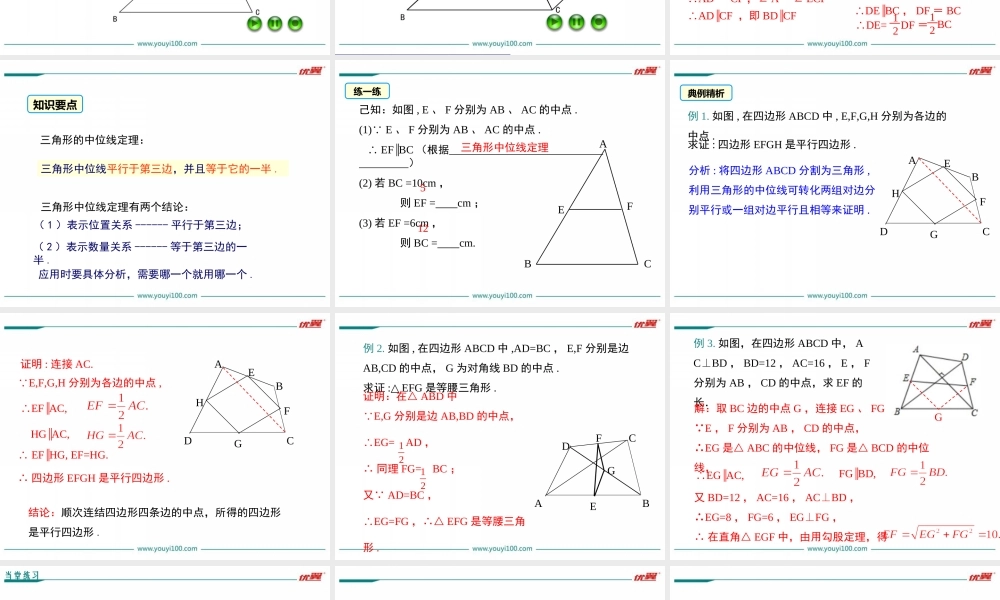
22.3三角形的中位线第二十二章四边形优翼课件导入新课讲授新课当堂练习课堂小结学练优八年级数学下(JJ)教学课件学习目标1.理解三角形中位线的概念,掌握三角形的中位线定理.(重点)2.能利用三角形的中位线定理解决有关证明和计算问题.(重点)导入新课复习引入ABC在三角形中,连结一个和它的的叫做三角形的中线.顶点顶点D中点DE是三角形的什么呢?E中点它就是我们这节课要学习的三角形的中位线.顶点对边中点线段讲授新课三角形的中位线定理观察与思考1.你能给“三角形中位线”下个定义吗?ABC中点D中点E2.一个三角形有几条中位线?3.三角形的中位线与中线有什么区别?答:三条.答:中位线是连接三角形两边中点的线段.中线是连结一个顶点和它的对边中点的线段.F定义:连接三角形两边中点的线段叫做三角形的中位线.1.剪一个三角形,记为△ABC;1.剪一个三角形,记为△ABC;2.分别取AB、AC的中点D、E,连结DE;3.沿DE将△ABC剪成两部分,并将△ADE绕点E旋转180度,得四边形BCFD.怎样将一张三角形的纸片剪成两部分,使分成的两部分能拼成一个平行四边形?动手操作议一议1.四边形BCFD是平行四边形吗?为什么?1.四边形BCFD是平行四边形吗?为什么?2.DE与BC有怎样的位置关系和数量关系?为什么?3.试猜想有关三角形中位线的性质.已知:如图,DE是△ABC的中位线求证:DEBC∥,DE=BC12BCADEBCF BD=AD=CF∴四边形BCFD是平行四边形∴DEBC∥,DF=BC证明:延长DE至F,使EF=DE,连接CF在△ADE和△CFE中AE=CE,∠AED=∠CEFEF=DE∴△ADE≌CFE△(SAS)∴AD=CF,∠A=∠ECF∴ADCF∥,即BDCF∥∴DE=DF=1212试一试三角形中位线平行于第三边,并且等于它的一半.知识要点三角形的中位线定理:三角形中位线定理有两个结论:(1)表示位置关系------平行于第三边;(2)表示数量关系------等于第三边的一半.应用时要具体分析,需要哪一个就用哪一个.练一练己知:如图,E、F分别为AB、AC的中点.(1)E 、F分别为AB、AC的中点.∴EFBC∥(根据)(2)若BC=10cm,则EF=cm;(3)若EF=6cm,则BC=cm.ABCEF三角形中位线定理512求证:四边形EFGH是平行四边形.例1.如图,在四边形ABCD中,E,F,G,H分别为各边的中点.分析:将四边形ABCD分割为三角形,利用三角形的中位线可转化两组对边分别平行或一组对边平行且相等来证明.典例精析ABCHDEFG证明:连接AC. E,F,G,H分别为各边的中点,∴EFHG,EF=HG.∥∴EFAC,∥HGAC,∥∴四边形EFGH是平行四边形.ABCHDEFG结论:顺次连结四边形四条边的中点,所得的四边形...