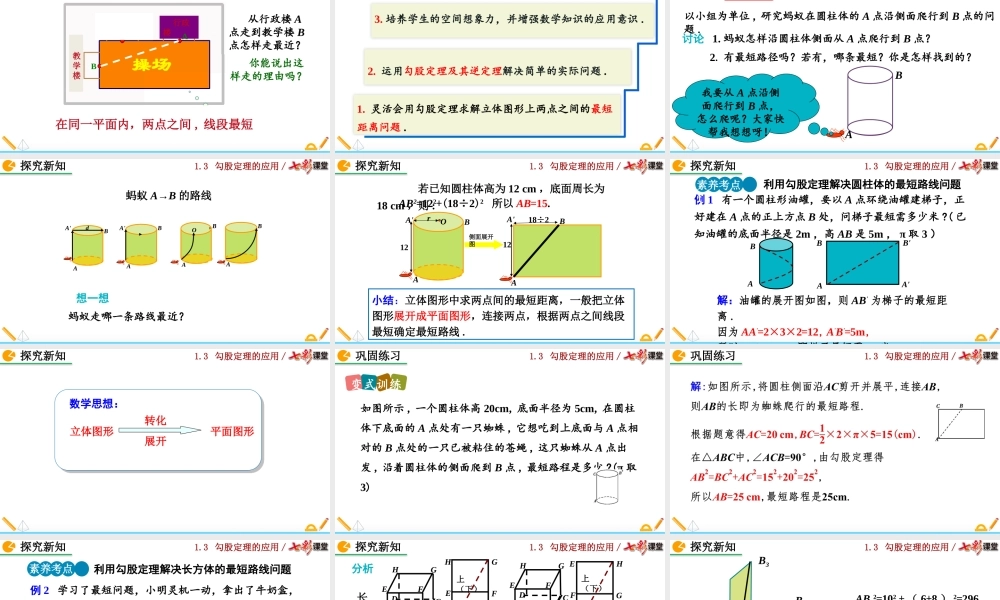
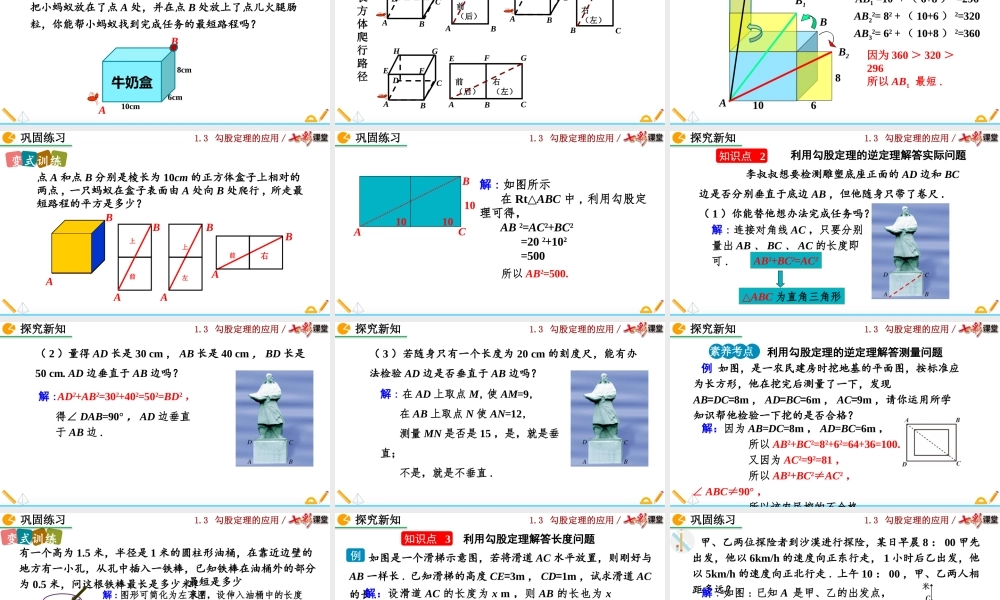
1.3勾股定理的应用/1.3勾股定理的应用北师大版数学八年级上册NEPQR121.3勾股定理的应用/在同一平面内,两点之间,线段最短从行政楼A点走到教学楼B点怎样走最近?教学楼行政楼BA你能说出这样走的理由吗?导入新知1.3勾股定理的应用/1.灵活会用勾股定理求解立体图形上两点之间的最短距离问题.2.运用勾股定理及其逆定理解决简单的实际问题.3.培养学生的空间想象力,并增强数学知识的应用意识.素养目标1.3勾股定理的应用/以小组为单位,研究蚂蚁在圆柱体的A点沿侧面爬行到B点的问题.讨论1.蚂蚁怎样沿圆柱体侧面从A点爬行到B点?2.有最短路径吗?若有,哪条最短?你是怎样找到的?BA我要从A点沿侧面爬行到B点,怎么爬呢?大家快帮我想想呀!探究新知知识点1利用勾股定理解答最短路径问题1.3勾股定理的应用/BAdABA'ABBAO想一想蚂蚁走哪一条路线最近?A'蚂蚁A→B的路线探究新知1.3勾股定理的应用/若已知圆柱体高为12cm,底面周长为18cm,则:BArO12侧面展开图1218÷2AB小结:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.A'A'AB2=122+(18÷2)2所以AB=15.探究新知1.3勾股定理的应用/例1有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米?(已知油罐的底面半径是2m,高AB是5m,π取3)ABABA'B'解:油罐的展开图如图,则AB'为梯子的最短距离.因为AA'=2×3×2=12,A'B'=5m,所以即梯子最短需米素养考点1利用勾股定理解决圆柱体的最短路线问题探究新知1.3勾股定理的应用/数学思想:立体图形平面图形转化展开探究新知1.3勾股定理的应用/如图所示,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蜘蛛,它想吃到上底面与A点相对的B点处的一只已被粘住的苍蝇,这只蜘蛛从A点出发,沿着圆柱体的侧面爬到B点,最短路程是多少?(π取3)3勾股定理的应用变式训练巩固练习1.3勾股定理的应用/3勾股定理的应用巩固练习1.3勾股定理的应用/B牛奶盒A例2学习了最短问题,小明灵机一动,拿出了牛奶盒,把小蚂蚁放在了点A处,并在点B处放上了点儿火腿肠粒,你能帮小蚂蚁找到完成任务的最短路程吗?6cm8cm10cm素养考点2利用勾股定理解决长方体的最短路线问题探究新知1.3勾股定理的应用/长方体爬行路径ABFEHGABCDEFGH前(后)上(下)ABCDEFGHBCGFEHABCDEFGH右(左)上(下)前(后)右(左)BCAEFG分析探究新知1.3勾股定理的应用/BB18AB2610B3AB12=102+(6+8)2=296AB22=82+...