专题 排列、组合——计数问题 课后练习二及详解.docVIP免费

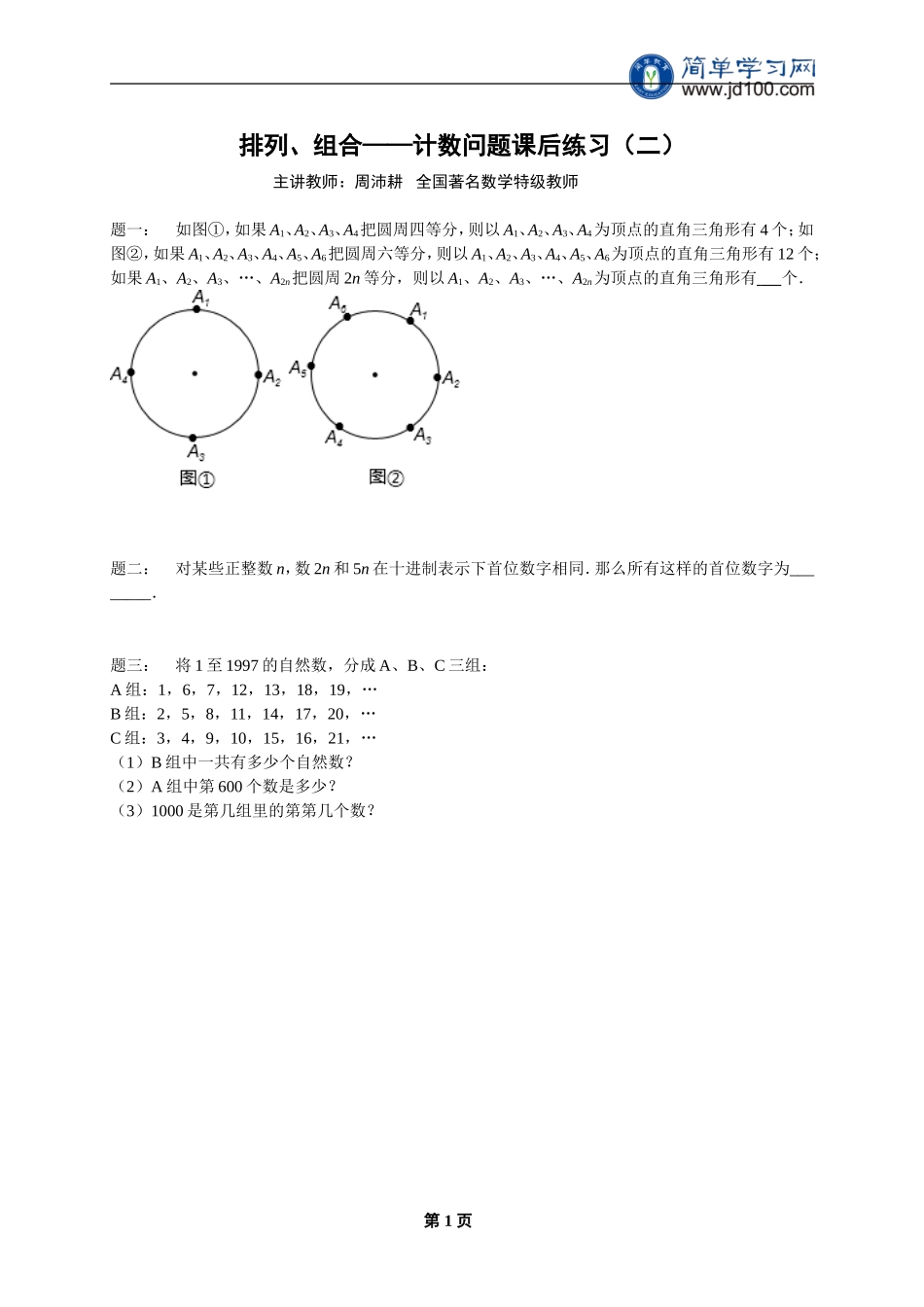
排列、组合——计数问题课后练习（二）主讲教师：周沛耕全国著名数学特级教师题一：如图①，如果A1、A2、A3、A4把圆周四等分，则以A1、A2、A3、A4为顶点的直角三角形有4个；如图②，如果A1、A2、A3、A4、A5、A6把圆周六等分，则以A1、A2、A3、A4、A5、A6为顶点的直角三角形有12个；如果A1、A2、A3、…、A2n把圆周2n等分，则以A1、A2、A3、…、A2n为顶点的直角三角形有个．题二：对某些正整数n，数2n和5n在十进制表示下首位数字相同．那么所有这样的首位数字为________．题三：将1至1997的自然数，分成A、B、C三组：A组：1，6，7，12，13，18，19，…B组：2，5，8，11，14，17，20，…C组：3，4，9，10，15，16，21，…（1）B组中一共有多少个自然数？（2）A组中第600个数是多少？（3）1000是第几组里的第第几个数？第1页排列、组合——计数问题课后练习参考答案题一：2n（n1）．详解：由圆周角定理知，直径所对的圆周角是直角．∴当A1、A2、A3、A4把圆周四等分时，该圆中的直径有A1A3，A2A4两条，∴①当以A1A3为直径时，有两个直角三角形；②当以A2A4为直径时，有两个直角三角形；∴如果A1、A2、A3、A4把圆周四等分，则以A1、A2、A3、A4为顶点的直角三角形有（4÷2）×（42）=4个；当A1、A2、A3、A4、A5、A6把圆周六等分，则以A1、A2、A3、A4、A5、A6为顶点的直角三角形有（6÷2）×（62）=12个；当A1、A2、A3、…、A2n把圆周2n等分，则以A1、A2、A3、…、A2n为顶点的直角三角形有（2n÷2）×（2n-2）=2n（n1）个．故答案是：2n（n1）．题二：3．详解：a×10k＜2n＜(a+1)×10k，a×10l＜5n＜(a+1)×10l，将两式相乘，得a2×10k+l＜10n＜(a+1)2×10k+l…①，注意到a2大于等于1，而(a+1)2小于等于100，于是10k+l＜10n＜10k+l+2，故n=k+1+1，从而①式变为a2＜10＜(a+1)2，解得a=3．故答案为3．题三：（1）666；（2）1800；（3）334．详解：（1）B组的数据排列的特点是，从第二个数开始，每个数减去2都是3的倍数，（1997-2）÷3=665，所以这串数字最后一项是1997，所以这组数中自然数一共有：（1997-2）÷3+1=666（个）；（2）A组数据中数的排列特点是：第2、4、6、8、10…个数分别是6的1、2、3、4、5…倍，所以第600个数是6的300倍，即300×6=1800；（3）C组数的排列规律：第1、3、5、7、9…个数分别是3的1、3、5、7、9…倍，第2、4、6、8、10…个数分别是前一个数加1得到的．1000÷3=333…1，所以1000是C组里的第334个数．第2页