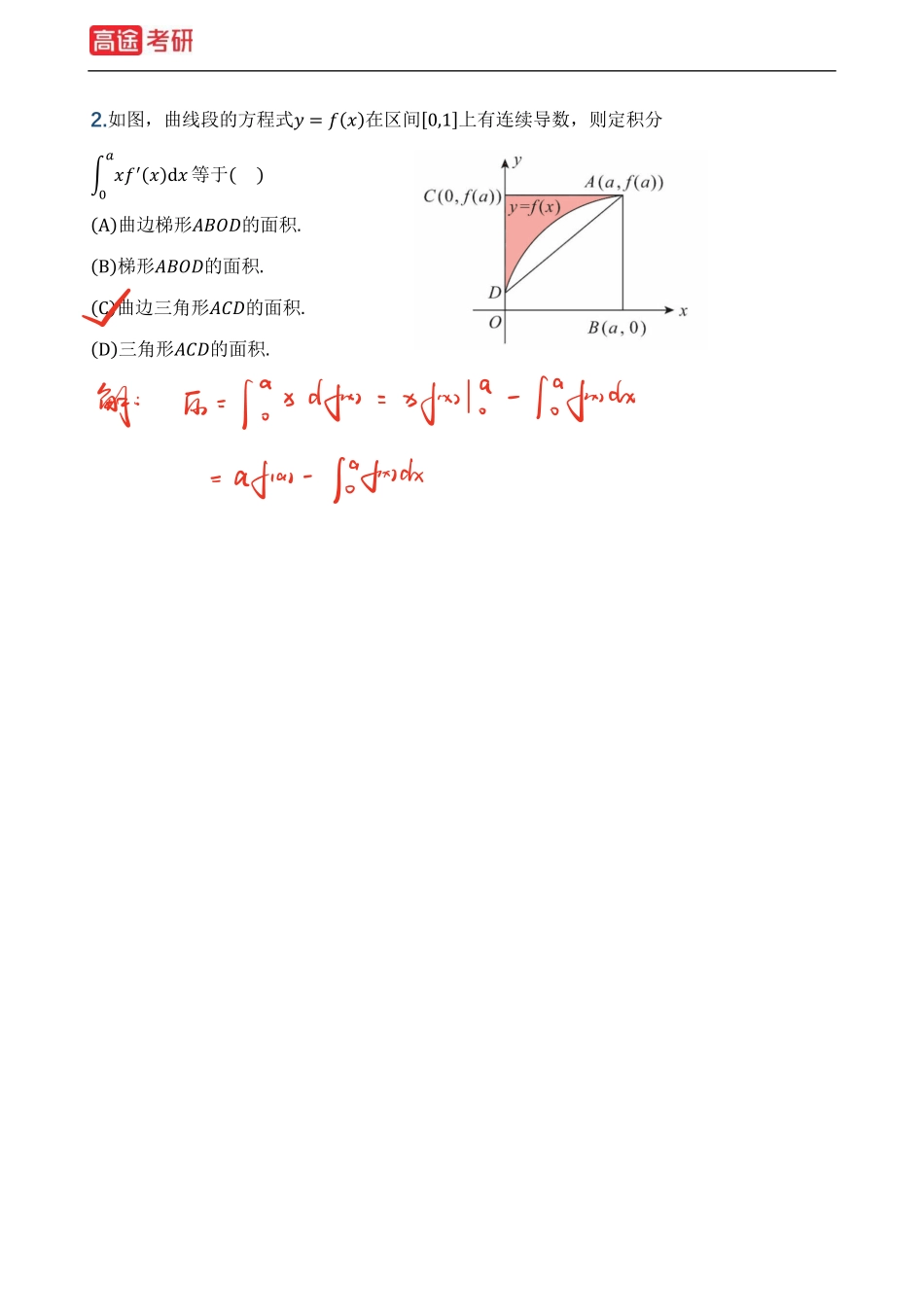
𝟏.已知函数𝑓(𝑥)=�2(𝑥−1),𝑥<1,ln𝑥,𝑥≥1,则𝑓(𝑥)的一个原函数是()(A)𝐹(𝑥)=�(𝑥−1)�,𝑥<1,𝑥(ln𝑥−1),𝑥≥1.(B)𝐹(𝑥)=�(𝑥−1)�,𝑥<1,𝑥(ln𝑥+1)−1,𝑥≥1.(C)𝐹(𝑥)=�(𝑥−1)�,𝑥<1,𝑥(ln𝑥+1)+1,𝑥≥1.(D)𝐹(𝑥)=�(𝑥−1)�,𝑥<1,𝑥(ln𝑥−1)+1,𝑥≥1.2.如图,曲线段的方程式𝑦=𝑓(𝑥)在区间[0,1]上有连续导数,则定积分�𝑥𝑓�(𝑥)d𝑥��等于()(A)曲边梯形𝐴𝐵𝑂𝐷的面积.(B)梯形𝐴𝐵𝑂𝐷的面积.(C)曲边三角形𝐴𝐶𝐷的面积.(D)三角形𝐴𝐶𝐷的面积.𝟑.设𝐼�=�𝑒��sin𝑥d𝑥���(𝑘=1,2,3),则()(A)𝐼�<𝐼�<𝐼�.(B)𝐼�<𝐼�<𝐼�.(C)𝐼�<𝐼�<𝐼�.(D)𝐼�<𝐼�<𝐼�.𝟒.求极限lim�→��𝑥��1+𝑥���d𝑥.𝟓.设𝑓(𝑥)是奇函数,除𝑥=0外处处连续,且𝑥=0是第一类间断点,则�𝑓(𝑡)d𝑡��是()(A)连续的奇函数.(B)在𝑥=0间断的奇函数.(C)连续的偶函数.(D)在𝑥=0间断的偶函数.𝟔.若ln�𝑥+�1+𝑥��为𝑓(𝑥)的一个原函数,求𝐼=�𝑥𝑓�(𝑥)d𝑥.𝟕.计算不定积分�𝑥ln𝑥(𝑥�−1)��d𝑥.𝟖.设𝐹(𝑥)是𝑓(𝑥)的原函数,且当𝑥≥0时,𝐹(𝑥)∙𝑓(𝑥)=𝑥𝑒�2(1+𝑥)�.已知𝐹(0)=1,𝐹(𝑥)>0,求𝑓(𝑥).𝟗.�𝑥sin�𝑥+𝑥�1+√1−𝑥�d𝑥���=.𝟏𝟎.�√1−sin2𝑥d𝑥���=.𝟏𝟏.�𝑥sin�𝑥d𝑥��=(𝑛≥1).𝟏𝟐.计算𝐼=�𝑒�1+𝑒�sin�𝑥d𝑥�����.𝟏𝟑.计算�𝑓(𝑥)√𝑥d𝑥��,其中𝑓(𝑥)=�ln(𝑡+1)𝑡d𝑡��.𝟏𝟒.若𝑓(𝑥)=𝑥1+cos�𝑥−�𝑓(𝑥)sin𝑥d𝑥���,求𝑓(𝑥).𝟏𝟓.设函数𝑓(𝑥)=�𝜆𝑒���,𝑥≥0,0,𝑥<0,(𝜆>0),则�𝑥𝑓(𝑥)����d𝑥=.𝟏.设𝑓(𝑥,𝑦)=�𝑥�𝑦𝑥�+𝑦�,(𝑥,𝑦)≠(0,0),0,(𝑥,𝑦)=(0,0),则𝑓(𝑥,𝑦)在(0,0)点处()(A)不连续.(B)连续但偏导数不存在.(C)偏导数存在但不可微.(D)可微.𝟐.设𝑓(𝑥,𝑦)=�𝑥�𝑦𝑥�+𝑦�,(𝑥,𝑦)≠(0,0),0,(𝑥,𝑦)=(0,0),求𝑓����(0,0)与𝑓����(0,0).𝟑.设𝑓(𝑥,𝑦)=|𝑥−𝑦|𝜑(𝑥,𝑦),其中𝜑(𝑥,𝑦)在点(0,0)的邻域内连续,问:(1)𝜑(𝑥,𝑦)应满足什么条件,可使𝑓��(0,0)和𝑓��(0,0)都存在;(2)在上述条件下𝑓(𝑥,𝑦)在点(0,0)是否可微.𝟒.设二元函数𝑧=ln(1+𝑥𝑦�),则𝜕�𝑧𝜕𝑥𝜕𝑦�(�,�)=.𝟓.设函数𝑓(𝑥,𝑦)=�𝑒���d𝑡���,则𝜕�𝑓𝜕𝑥𝜕𝑦�(�,�)=.𝟔.设𝑢=𝑓(𝑥,𝑦,𝑧),𝑦=𝜑(𝑥,𝑡),𝑡=𝜓(𝑥,𝑧),其中𝑓,𝑦,𝜓可微,求∂𝑢∂𝑥,∂𝑢∂z.𝟕.设函数𝑓(𝑢,𝑣...