高数第十章数一专题讲义-赵老师【公众号：小盆学长】免费分享.pdfVIP免费

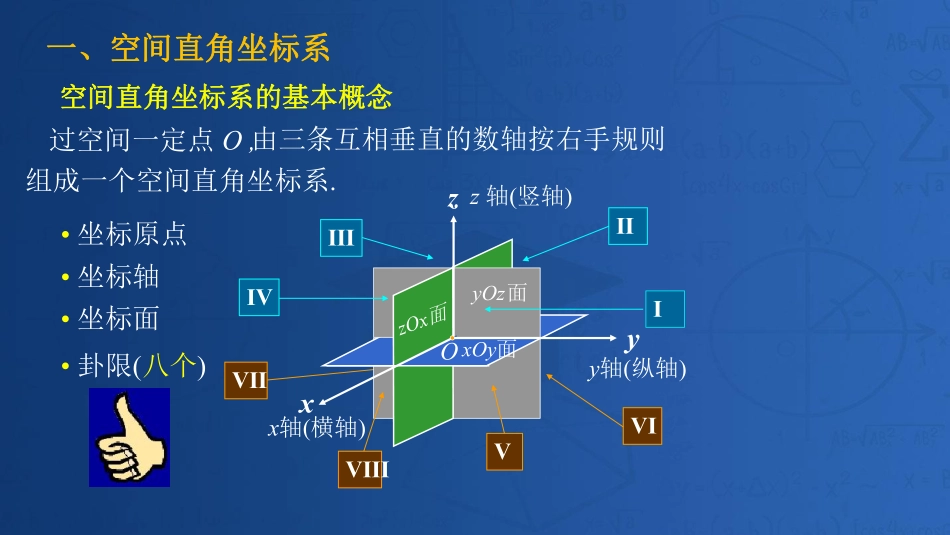
赵军高等数学零基础课程ⅦⅡⅢⅥxyzⅤⅧⅣ一、空间直角坐标系由三条互相垂直的数轴按右手规则组成一个空间直角坐标系.•坐标原点•坐标轴x轴(横轴)y轴(纵轴)z轴(竖轴)过空间一定点O,•坐标面•卦限(八个)空间直角坐标系的基本概念ⅠO面xOy面yOzzOx面在直角坐标系下xyz向径11坐标轴上的点P,Q,R;坐标面上的点A,B,C点M特殊点的坐标:有序数组),,(zyx11)0,0,(xP)0,,0(yQ),0,0(zR),,0(zyB(称为点M的坐标)原点O(0,0,0);rOr)0,,(yxAM),0,(zxC坐标轴:轴x00zy00xz轴y轴z00yx坐标面:xOy面0zyOz面0xzOx面0yxyzO二、向量1.向量的基本概念向量:既有大小,又有方向的量称为向量1M2M向量的模:向量的大小,,21MM记作单位向量:模为1的向量,零向量:模为0的向量,记作e或e..00或，记作规定:零向量与任何向量平行;若向量a与b大小相等,方向相同,则称a与b相等,记作a＝b;若向量a与b方向相同或相反,则称a与b平行,a∥b;与a的模相同,但方向相反的向量称为a的负向量,记作因平行向量可平移到同一直线上,故两向量平行又称两向量共线.若k(≥3)个向量经平移可移到同一平面上,则称此k个向量共面.记作－a;2.向量的坐标表示在空间直角坐标系下,设点M,),,(zyxM则沿三个坐标轴方向的分向量,),,(zyxxOyzMNBCA,,,,,轴上的单位向量分别表示以zyxkji的坐标为此式称为向量r的坐标分解式,任意向量r可用向径OM表示.NMONOMOCOBOA记,ixOA,jyOBrkzjyix称为向量,,kzOCkzjyixrikjr.,,的坐标称为向量rzyx3.向量的线性运算则),,(zzyyxxbababa),,(zyxaaa，为实数设),,,(zyxaaaa,),,(zyxbbbbbaa4.向量的模、方向角、方向余弦222zyxxOyzMQR),,,(zyxr设OMrOyzx与三坐标轴的夹角,,为其方向角.cos222zyxx方向角的余弦称为其方向余弦.,0),,(zyxr给定r称rxrOyzxrcos222zyxxcos222zyxycos222zyxz1coscoscos222方向余弦的性质:)cos,cos,(cosrxryrzrrer:的单位向量向量r例1.已知两点)2,2,2(1M和,)0,3,1(2M的模、方向余弦和方向角.解:,21,23)20计算向量)2,1,1(222)2(1)1(2,21cos,21cos22cos,3π2,3π4π321MM(21MM21MM三、向量的内积、外积、混合积1.向量的内积（数量积）定义设向量的夹角为,称记作数量积(点积).bacosba的与为baba,...