第二章第四节　 指数与指数函数.pptVIP免费

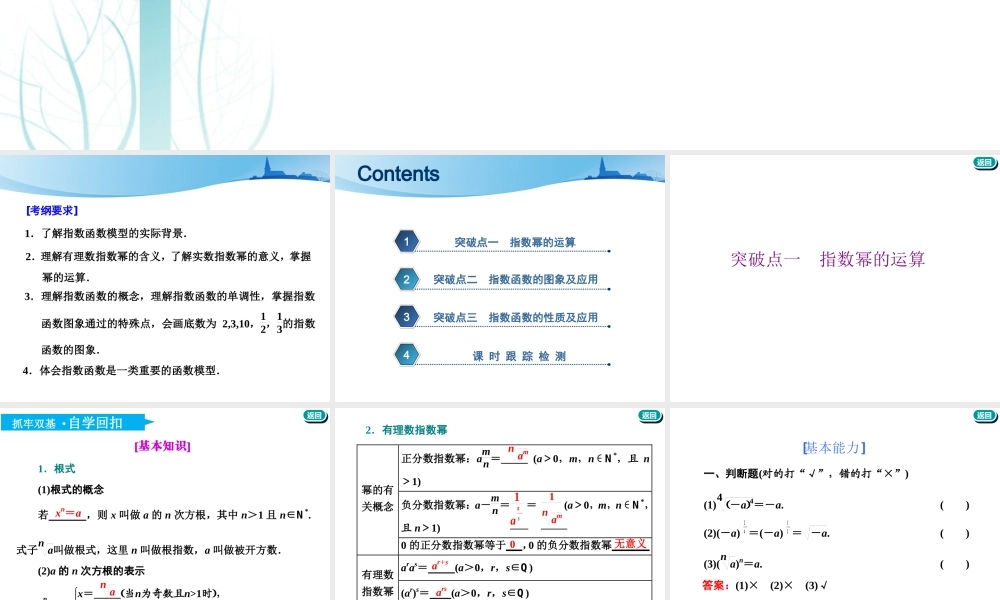
第四节指数与指数函数[考纲要求]1．了解指数函数模型的实际背景．2．理解有理数指数幂的含义，了解实数指数幂的意义，掌握幂的运算．3．理解指数函数的概念，理解指数函数的单调性，掌握指数函数图象通过的特殊点，会画底数为2,3,10，12，13的指数函数的图象．4．体会指数函数是一类重要的函数模型．1234Contents突破点一指数幂的运算突破点二指数函数的图象及应用突破点三指数函数的性质及应用课时跟踪检测返回返回突破点一指数幂的运算返回返回抓牢双基·自学回扣[基本知识]1．根式(1)根式的概念若，则x叫做a的n次方根，其中n＞1且n∈N*.式子na叫做根式，这里n叫做根指数，a叫做被开方数．(2)a的n次方根的表示xn＝a⇒x＝_____当n为奇数且n>1时，x＝______当n为偶数且n>1时.xn＝ana±na返回返回2．有理数指数幂正分数指数幂：amn＝_____(a＞0，m，n∈N*，且n＞1)负分数指数幂：a－mn＝＝(a＞0，m，n∈N*，且n＞1)幂的有关概念0的正分数指数幂等于___，0的负分数指数幂_______aras＝(a＞0，r，s∈Q)(ar)s＝(a＞0，r，s∈Q)有理数指数幂的性质(ab)r＝(a＞0，b＞0，r∈Q)nam1amn1nam0无意义ar＋sarsarbr返回返回[基本能力]一、判断题(对的打“√”，错的打“×”)(1)4－a4＝－a.()(2)(－a)24＝(－a)12＝－a.()(3)(na)n＝a.()答案：(1)×(2)×(3)√返回返回二、填空题1．计算：π0＋2－2×21412＝________.答案：1182．设a>0，将a2a·3a2表示成分数指数幂的形式，其结果是________．解析：a2a·3a2＝a2a·a23＝a2a53＝a2a51×32＝a2·a56＝a2526＝a76.答案：a76返回返回3．若2a－12＝31－2a3，则实数a的取值范围为________．解析：2a－12＝|2a－1|，31－2a3＝1－2a.因为|2a－1|＝1－2a.故2a－1≤0，所以a≤12.答案：－∞，12返回返回研透高考·深化提能指数幂的运算规律(1)有括号的先算括号里的，无括号的先进行指数运算．(2)先乘除后加减，负指数幂化成正指数幂的倒数．(3)底数是负数，先确定符号，底数是小数，先化成分数，底数是带分数的，先化成假分数．(4)若是根式，应化为分数指数幂，尽可能用幂的形式表示，运用指数幂的运算性质来解答．返回返回[典例](1)a3a·5a4(a>0)的值是()A．1B．aC．a15D．a1710[解析]a3a·5a4＝a3a12·a45＝a143--25＝a1710.故选D.[答案]D返回返回(2)2350＋2－2·21412－(0.01)0.5＝________.[解析]原式＝1＋14×...