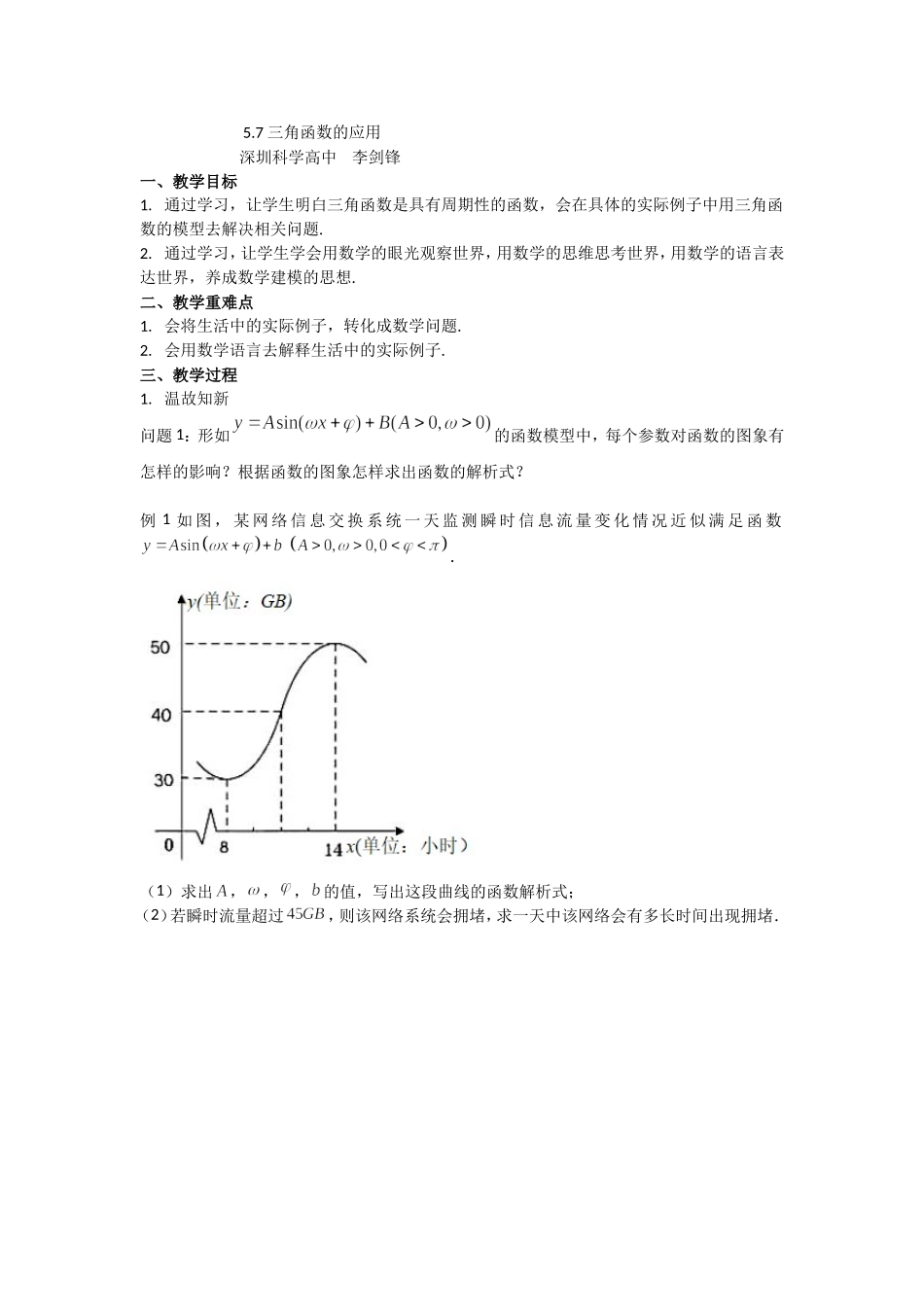
5.7三角函数的应用深圳科学高中李剑锋一、教学目标1.通过学习,让学生明白三角函数是具有周期性的函数,会在具体的实际例子中用三角函数的模型去解决相关问题.2.通过学习,让学生学会用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界,养成数学建模的思想.二、教学重难点1.会将生活中的实际例子,转化成数学问题.2.会用数学语言去解释生活中的实际例子.三、教学过程1.温故知新问题1:形如的函数模型中,每个参数对函数的图象有怎样的影响?根据函数的图象怎样求出函数的解析式?例1如图,某网络信息交换系统一天监测瞬时信息流量变化情况近似满足函数.(1)求出,,,的值,写出这段曲线的函数解析式;(2)若瞬时流量超过,则该网络系统会拥堵,求一天中该网络会有多长时间出现拥堵.配套练习(1)已知函数的部分图像如图所示.(1)写出的最小正周期及其单调递减区间;(2)求的解析式;(3)若要得到的图像,只需要函数的图像经过怎样的图像变换?小结:形如的函数模型中,问题2:在实际的生活情境中,怎么建立函数模型?如何利用数学模型并应用数学知识解决实际问题?例2.如图所示,秒针尖的位置为,若初始位置为,当秒针从(此时)正常开始走时,那么点M的横坐标与时间t的函数关系为()A.B.C.D.配套练习(2)摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢往上转,可以从高处俯瞰四周景色.位于潍坊滨海的“渤海之眼”摩天轮是世界上最大的无轴摩天轮,该摩天轮轮盘直径为124米,设置有36个座舱.游客在座舱转到距离地面最近的位置进舱,当到达最高点时距离地面145米,匀速转动一周大约需要30分钟.当游客甲坐上摩天轮的座舱开始计时.(1)经过t分钟后游客甲距离地面的高度为H米,已知H关于t的函数关系式满足(其中,,)求摩天轮转动一周的解析式;(2)游客甲坐上摩天轮后多长时间,距离地面的高度第一次恰好达到52米?(3)若游客乙在游客甲之后进入座舱,且中间间隔5个座舱,在摩天轮转动一周的过程中,记两人距离地面的高度差为h米,求h的最大值.例3.设是某港口水的深度(米)关于时刻(时)的函数,其中.下表是该港口某一天从到时记录的时刻与水深的关系,经长期观测,函数的图象可以近似地看成函数的图象.下面的函数中,最能近似地表示表中数据间对应关系的是A.,B.,C.,,D.,配套练习(3)为了迎接旅游旺季的到来,少林寺设置了一个专门安排旅客住宿的客栈,寺庙的工作人员发现...