《二次函数的应用（1）》教学课件.pptVIP免费

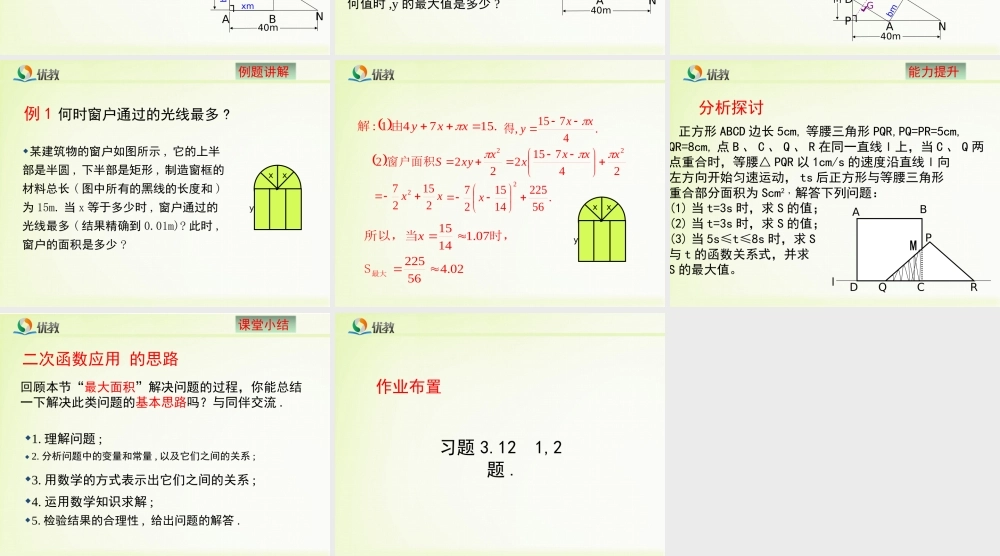
第三章二次函数6.二次函数的应用（1）Contents目录01020304课堂小结05能力提升合作探究例题讲解问题引入问题引入用48米长的竹篱笆围建一矩形养鸡场,养鸡场一面用砖砌成,另三面用竹篱笆围成,并且在与砖墙相对的一面开2米宽的门(不用篱笆),问养鸡场的边长为多少米时,养鸡场占地面积最大?最大面积是多少?2mym2xmxm合作探究(1).设矩形的一边AB=xm,那么AD边的长度如何表示？(2).设矩形的面积为ym2,当x取何值时,y的值最大？最大值是多少?何时面积最大？如图,在一个直角三角形的内部作一个矩形ABCD，其中AB和AD分别在两直角边上.MN40m30mABCD┐想一想ABCD┐MN.3043,.1:xbbmAD易得设解40m30mxxxxxby30433043.22.30020432x.30044,202:2abacyabx最大值时当或用公式xmbm(1).设矩形的一边BC=xm,那么AB边的长度如何表示？(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?如图,在一个直角三角形的内部作一个矩形ABCD，其中点A和点D分别在两直角边上,BC在斜边上.ABCD┐MNP40m30mxmbmHG┛┛议一议.24,50.1:mPHmMN由勾股定理得解xxxxxby242512242512.22.3002525122x.30044,252:2abacyabx最大值时当或用公式.242512,xbbmAB易得设ABCD┐MNP40m30mxmbmHG┛┛例题讲解何时窗户通过的光线最多?某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?xxy例1xxy.1574.1:xxy由解.4715,xxy得xx21527224715222.222xxxxxxyS窗户面积.562251415272x02.45622507.11415最大S时，所以，当x能力提升正方形ABCD边长5cm,等腰三角形PQR,PQ=PR=5cm,QR=8cm,点B、C、Q、R在同一直线l上，当C、Q两点重合时，等腰△PQR以1cm/s的速度沿直线l向左方向开始匀速运动，ts后正方形与等腰三角形重合部分面积为Scm2，解答下列问题：(1)当t=3s时，求S的值；(2)当t=3s时，求S的值；(3)当5s≤t≤8s时，求S与t的函数关系式，并求S的最大值。MABCDPQRl分析探讨课堂小结1.理解问题;二次函数应用的思路回顾本节“最大面积”解决问题的过程，你能总结一下解决此类问题的基本思路吗？与同伴交流.2.分析问题中的变量和常量,以及它们之间的关系;3.用数学的方式表示出它们之间的关系;4.运用数学知识求解;5.检验结果的合理性,给出问题的解答.习题3.121,2题.作业布置