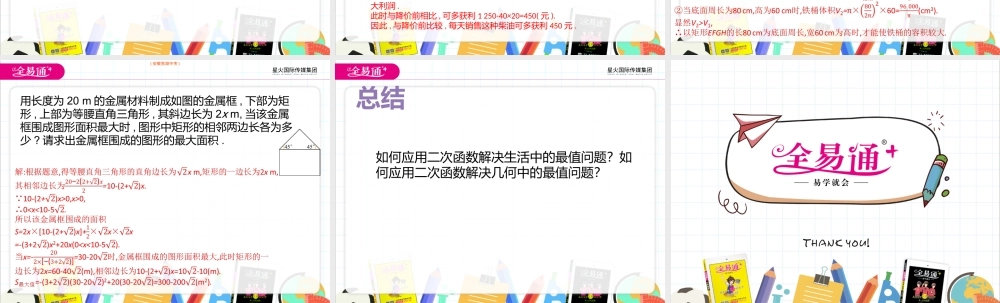
5.7二次函数的应用(1)会应用二次函数解决生活中的最值问题。学习目标练习1.判断正误:(1)在实际问题中,二次函数的最值不一定是实际问题的最值.()(2)若实际问题中的二次函数图象开口向下,则这个实际问题只有最大值,无最小值.()(3)当3≤x≤5时,二次函数y=x2-4x-5的最小值是0.()2.某种商品每件进价20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30-x)件,若使利润最大,每件的售价应为元.1.(1))√(2)✕(3)✕2.25练习利用二次函数的最值解答商品销售中的“最大利润”问题时,可采用以下步骤:(1)设出自变量,用含自变量的代数式表示销售单价、销售量或销售额.(2)用含自变量的代数式表示销售商品的成本.(3)用因变量及含自变量的代数式分别表示销售利润,即可得到函数表达式.(4)根据函数表达式求出最值及取得最值时自变量的值.某地有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克放入冷藏室中,据预测,每千克该野生菌的市场价格每天将上涨1元,但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这种野生菌在冷藏室中最多只能保存160天.同时,平均每天有3千克的野生菌因损坏而不能出售.(1)设x天后每千克野生菌的市场价格为y元,试写出y与x之间的函数表达式;(2)若存放x天后,将这批野生菌一次性出售,设这批野生菌的销售总额为p元,试写出p与x之间的函数表达式;(3)李经理将这批野生菌存放多少天后出售可获得最大利润(利润=销售总额-收购成本-各种费用)?最大利润是多少?解:(1)由题意,得y=x+30(1≤x≤160,且x为整数).(2)p=y·(1000-3x)=-3x2+910x+30000(1≤x≤160,且x为整数).(3)利润W=p-30×1000-310x=-3(x-100)2+30000(1≤x≤160),当x=100时,W最大=30000.所以李经理将这批野生菌存放100天后出售可获得最大利润,最大利润是30000元.某超市购进商品的单价是8元/件,当售价为10元/件时,售出200件,销售单价每提高2元,售出数量就减少10件,现要使售货的金额最大,销售单价应定为多少元?(湖北咸宁中考)某农机服务站销售一批柴油,平均每天可售出20桶,每桶盈利40元.为了支援我市抗旱救灾,农机服务站决定采取降价措施.经市场调研发现:如果每桶柴油降价1元,农机服务站平均每天可多售出2桶.(1)假设每桶柴油降价x元,每天销售这种柴油所获利润为y元,求y与x之间的函数关系式;(2)每桶柴油降价多少元后出售,农机服务站每天销售这种柴油可获得最大利润?此时,与降价前比较,每天销售这种柴油可多获利多少元?解:(1)y=(4...