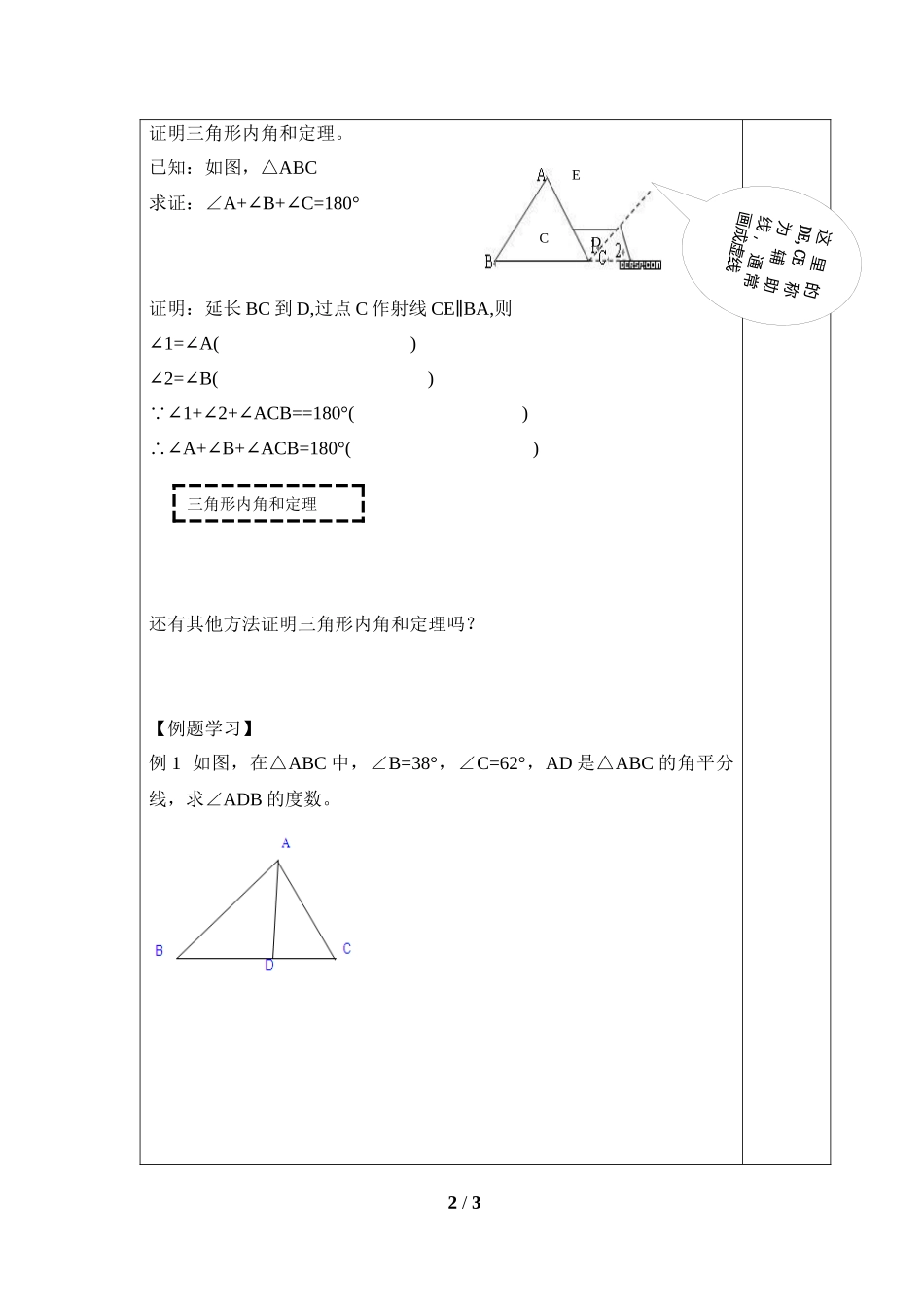
1/3班级:姓名:科目数学课题8.6三角形内角和定理(1)授课时间学习目标1、掌握三角形内角和定理及证明。2、初步学会利用辅助线证明,同时培养学生观察、猜想、和论证能力。3、进一步理解证明的步骤、格式和方法,发展演绎推理能力。学习重、难点重点:三角形内角和定理的证明思路及应用。难点:三角形内角和定理的证明方法。【温故知新】一、预习课本51页---53页内容。二、预习检测:1、我们知道三角形的内角和等于,即三角形三个内角和等于角,你能验证这个结论吗?2、用准备好的三角形硬纸片剪纸拼图,如图,把∠A剪下放在位置上,∠B剪下放在位置上,较直观得到三角形内角和是。注意:实验得出的命题,不能当做定理。那么,怎样来证明这一结论呢?3、学生回忆证明一个命题的步骤:(1);(2);(3);(4);(5);(6);【合作探究】合作探究一:同步导学2/3证明三角形内角和定理。已知:如图,△ABC求证:∠A+B+C=180°∠∠证明:延长BC到D,过点C作射线CEBA,∥则1=A()∠∠2=B()∠∠∵1+2+ACB==180°()∠∠∠∴A+B+ACB=180°()∠∠∠还有其他方法证明三角形内角和定理吗?【例题学习】例1如图,在△ABC中,∠B=38°,∠C=62°,AD是△ABC的角平分线,求∠ADB的度数。三角形内角和定理这里的DE,CE称为辅助线,通常画成虚线EDC3/3【课堂检测】如图,已知∠AMN+MNF+NFC=360°∠∠,求证:ABCD(∥用两种方法证明)【学习反思】