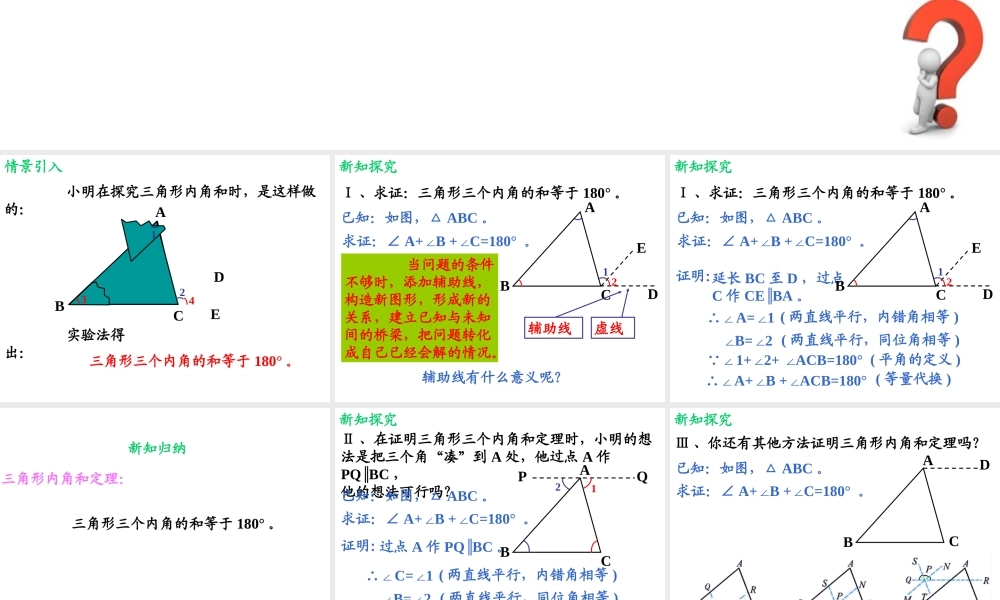
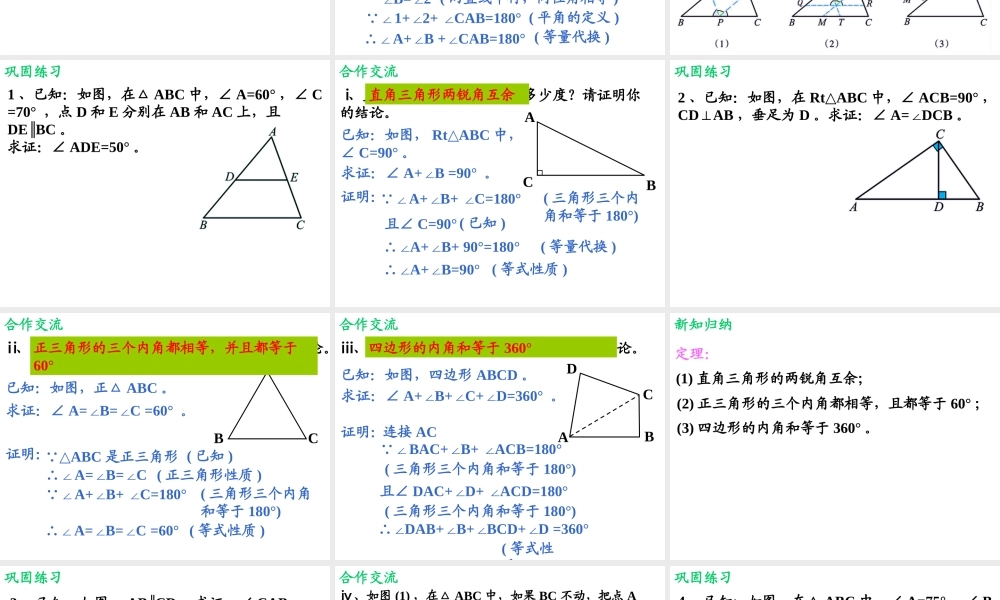
8.6三角形内角和定理(1)8.6三角形内角和定理(1)小明在探究三角形内角和时,是这样做的:情景引入ABC3412DE实验法得出:三角形三个内角的和等于180°。Ⅰ、求证:三角形三个内角的和等于180°。新知探究已知:如图,△ABC。求证:∠A+B+C=180°∠∠。ABCDE辅助线辅助线有什么意义呢?虚线12当问题的条件不够时,添加辅助线,构造新图形,形成新的关系,建立已知与未知间的桥梁,把问题转化成自己已经会解的情况。Ⅰ、求证:三角形三个内角的和等于180°。新知探究已知:如图,△ABC。求证:∠A+B+C=180°∠∠。证明:∴∠A=1∠(两直线平行,内错角相等)延长BC至D,过点C作CEBA∥。 ∠1+2+ACB=180°∠∠(平角的定义)∴∠A+B+ACB=180°∠∠(等量代换)ABC∠B=2∠(两直线平行,同位角相等)DE12新知归纳三角形内角和定理:三角形三个内角的和等于180°。Ⅱ、在证明三角形三个内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作PQBC∥,他的想法可行吗?新知探究已知:如图,△ABC。求证:∠A+B+C=180°∠∠。证明:∴∠C=1∠(两直线平行,内错角相等)过点A作PQBC∥。 ∠1+2+CAB=180°∠∠(平角的定义)∴∠A+B+CAB=180°∠∠(等量代换)ABC∠B=2∠(两直线平行,同位角相等)PQ21Ⅲ、你还有其他方法证明三角形内角和定理吗?已知:如图,△ABC。求证:∠A+B+C=180°∠∠。ABC新知探究D1、已知:如图,在△ABC中,∠A=60°,∠C=70°,点D和E分别在AB和AC上,且DEBC∥。求证:∠ADE=50°。巩固练习合作交流ⅰ、直角三角形的两锐角和是多少度?请证明你的结论。ABC已知:如图,RtABC△中,∠C=90°。求证:∠A+B=90°∠。证明: ∠A+B+C=180°∠∠(三角形三个内角和等于180°)且∠C=90°(已知)∴∠A+B+90°=180°∠(等量代换)∴∠A+B=90°∠(等式性质)直角三角形两锐角互余2、已知:如图,在RtABC△中,∠ACB=90°,CDAB⊥,垂足为D。求证:∠A=DCB∠。巩固练习合作交流ⅱ、正三角形的一个内角是多少度?证明你的结论。ABC已知:如图,正△ABC。求证:∠A=B=C∠∠=60°。证明: ∠A+B+C=180°∠∠(三角形三个内角和等于180°) △ABC是正三角形(已知)∴∠A=B=C∠∠(正三角形性质)∴∠A=B=C∠∠=60°(等式性质)正三角形的三个内角都相等,并且都等于60°合作交流ⅲ、四边形的内角和是多少度?证明你的结论。ABCD已知:如图,四边形ABCD。求证:∠A+B+C+D=360°∠∠∠。证明: ∠BAC+B+ACB=180°∠∠(三角形三个内角和等于180°)连接AC且∠DAC+D...