高一数学人教版A版必修二课件：4.3.2 空间两点间的距离公式 .pptxVIP免费

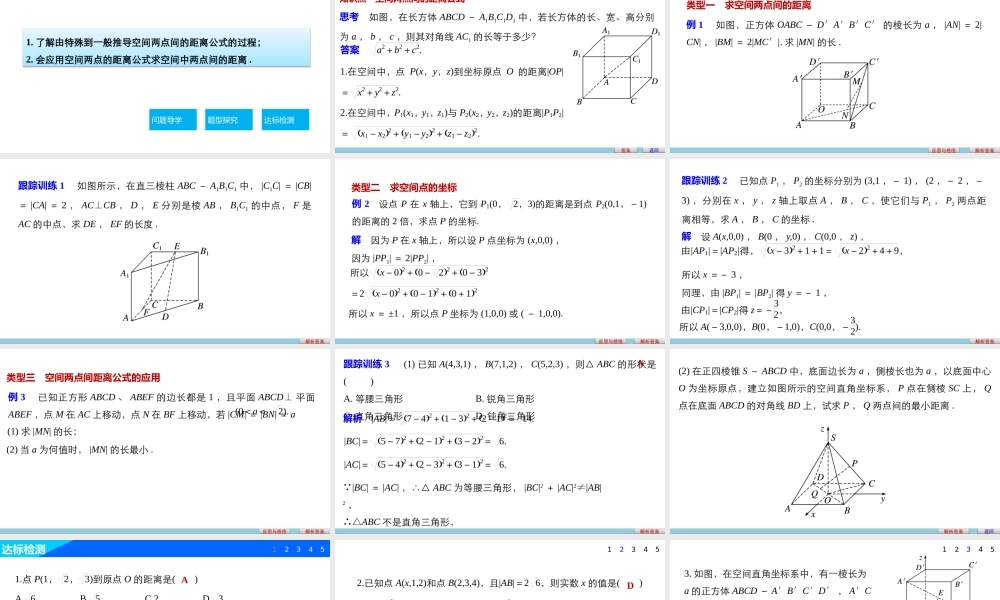
第四章§4.3空间直线坐标系4.3.2空间两点间的距离公式1.了解由特殊到一般推导空间两点间的距离公式的过程；2.会应用空间两点的距离公式求空间中两点间的距离.问题导学题型探究达标检测学习目标问题导学新知探究点点落实知识点空间两点间的距离公式思考如图，在长方体ABCD－A1B1C1D1中，若长方体的长、宽、高分别为a，b，c，则其对角线AC1的长等于多少？答案答案a2＋b2＋c2.1.在空间中，点P(x，y，z)到坐标原点O的距离|OP|＝x2＋y2＋z2.2.在空间中，P1(x1，y1，z1)与P2(x2，y2，z2)的距离|P1P2|＝x1－x22＋y1－y22＋z1－z22.返回题型探究重点难点个个击破类型一求空间两点间的距离例1如图，正方体OABC－D′A′B′C′的棱长为a，|AN|＝2|CN|，|BM|＝2|MC′|.求|MN|的长.反思与感悟解析答案跟踪训练1如图所示，在直三棱柱ABC－A1B1C1中，|C1C|＝|CB|＝|CA|＝2，AC⊥CB，D，E分别是棱AB，B1C1的中点，F是AC的中点，求DE，EF的长度.解析答案类型二求空间点的坐标解因为P在x轴上，所以设P点坐标为(x,0,0)，因为|PP1|＝2|PP2|，解析答案例2设点P在x轴上，它到P1(0，2，3)的距离是到点P2(0,1，－1)的距离的2倍，求点P的坐标.所以x－02＋0－22＋0－32＝2x－02＋0－12＋0＋12所以x＝±1，所以点P坐标为(1,0,0)或(－1,0,0).反思与感悟跟踪训练2已知点P1，P2的坐标分别为(3,1，－1)，(2，－2，－3)，分别在x，y，z轴上取点A，B，C，使它们与P1，P2两点距离相等，求A，B，C的坐标.解设A(x,0,0)，B(0，y,0)，C(0,0，z)，解析答案由|AP1|＝|AP2|得，x－32＋1＋1＝x－22＋4＋9，所以x＝－3，同理，由|BP1|＝|BP2|得y＝－1，由|CP1|＝|CP2|得z＝－32，所以A(－3,0,0)，B(0，－1,0)，C(0,0，－32).类型三空间两点间距离公式的应用例3已知正方形ABCD、ABEF的边长都是1，且平面ABCD⊥平面ABEF，点M在AC上移动，点N在BF上移动，若|CM|＝|BN|＝a解析答案＜a＜2).(0(1)求|MN|的长；(2)当a为何值时，|MN|的长最小.反思与感悟跟踪训练3(1)已知A(4,3,1)，B(7,1,2)，C(5,2,3)，则△ABC的形状是()A.等腰三角形B.锐角三角形C.直角三角形D.钝角三角形解析答案解析|AB|＝7－42＋1－32＋2－12＝14.|AC|＝5－42＋2－32＋3－12＝6. |BC|＝|AC|，∴△ABC为等腰三角形，|BC|2＋|AC|2≠|AB|2，∴△ABC不是直角三角形，A|BC|＝5－72＋2－12＋3－22＝6.(2)在正四棱锥S－ABCD中，底面边长为a，侧棱长也为...