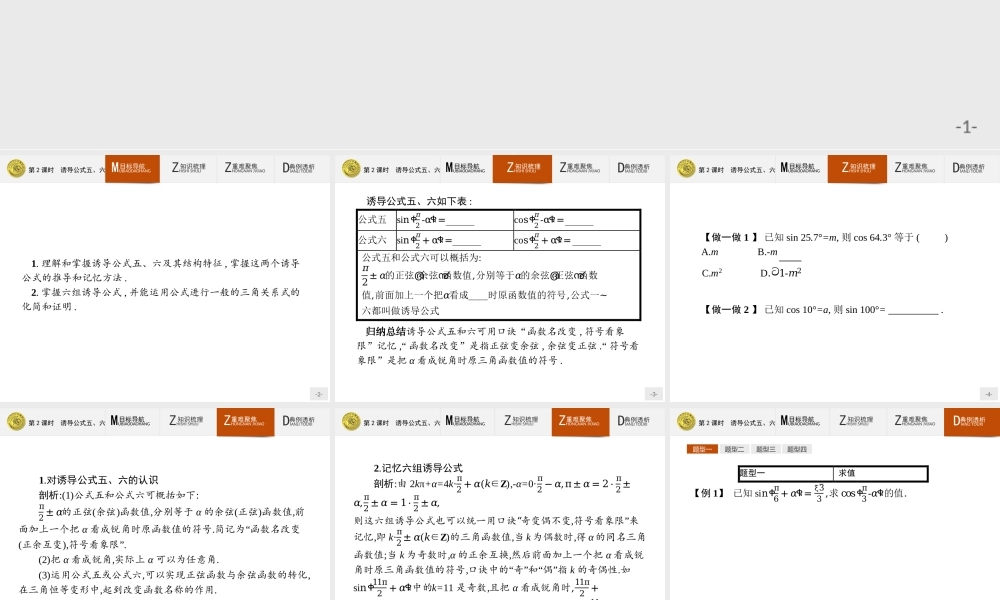
-1-第2课时诱导公式五、六-2-第2课时诱导公式五、六ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航1.理解和掌握诱导公式五、六及其结构特征,掌握这两个诱导公式的推导和记忆方法.2.掌握六组诱导公式,并能运用公式进行一般的三角关系式的化简和证明.-3-第2课时诱导公式五、六ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航诱导公式五、六如下表:归纳总结诱导公式五和六可用口诀“函数名改变,符号看象限”记忆,“函数名改变”是指正弦变余弦,余弦变正弦.“符号看象限”是把α看成锐角时原三角函数值的符号.公式五sinቀ𝜋2-αቁ=cos𝛼cosቀ𝜋2-αቁ=sin𝛼公式六sinቀ𝜋2+αቁ=cos𝛼cosቀ𝜋2+αቁ=−sin𝛼公式五和公式六可以概括为:𝜋2±𝛼的正弦൫余弦൯函数值,分别等于𝛼的余弦൫正弦൯函数值,前面加上一个把𝛼看成锐角时原函数值的符号,公式一~六都叫做诱导公式-4-第2课时诱导公式五、六ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航【做一做1】已知sin25.7°=m,则cos64.3°等于()A.mB.-m答案:A【做一做2】已知cos10°=a,则sin100°=.答案:aC.m2D.ට1-𝑚2-5-第2课时诱导公式五、六ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航1.对诱导公式五、六的认识剖析:(1)公式五和公式六可概括如下:π2±𝛼的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号.简记为“函数名改变(正余互变),符号看象限”.(2)把α看成锐角,实际上α可以为任意角.(3)运用公式五或公式六,可以实现正弦函数与余弦函数的转化,在三角恒等变形中,起到改变函数名称的作用.-6-第2课时诱导公式五、六ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航2.记忆六组诱导公式剖析:由2kπ+α=4k·π2+𝛼(𝑘∈Z),-α=0·π2−𝛼,π±𝛼=2·π2±𝛼,π2±𝛼=1·π2±𝛼,则这六组诱导公式也可以统一用口诀“奇变偶不变,符号看象限”来记忆,即k·π2±𝛼(𝑘∈Z)的三角函数值,当k为偶数时,得α的同名三角函数值;当k为奇数时,α的正余互换,然后前面加上一个把α看成锐角时原三角函数值的符号,口诀中的“奇”和“偶”指k的奇偶性.如sinቀ11π2+𝛼ቁ中的k=11是奇数,且把α看成锐角时,11π2+𝛼是第四象限角,第四象限角的正弦值是负数,所以sinቀ11π2+𝛼ቁ=−cosα...