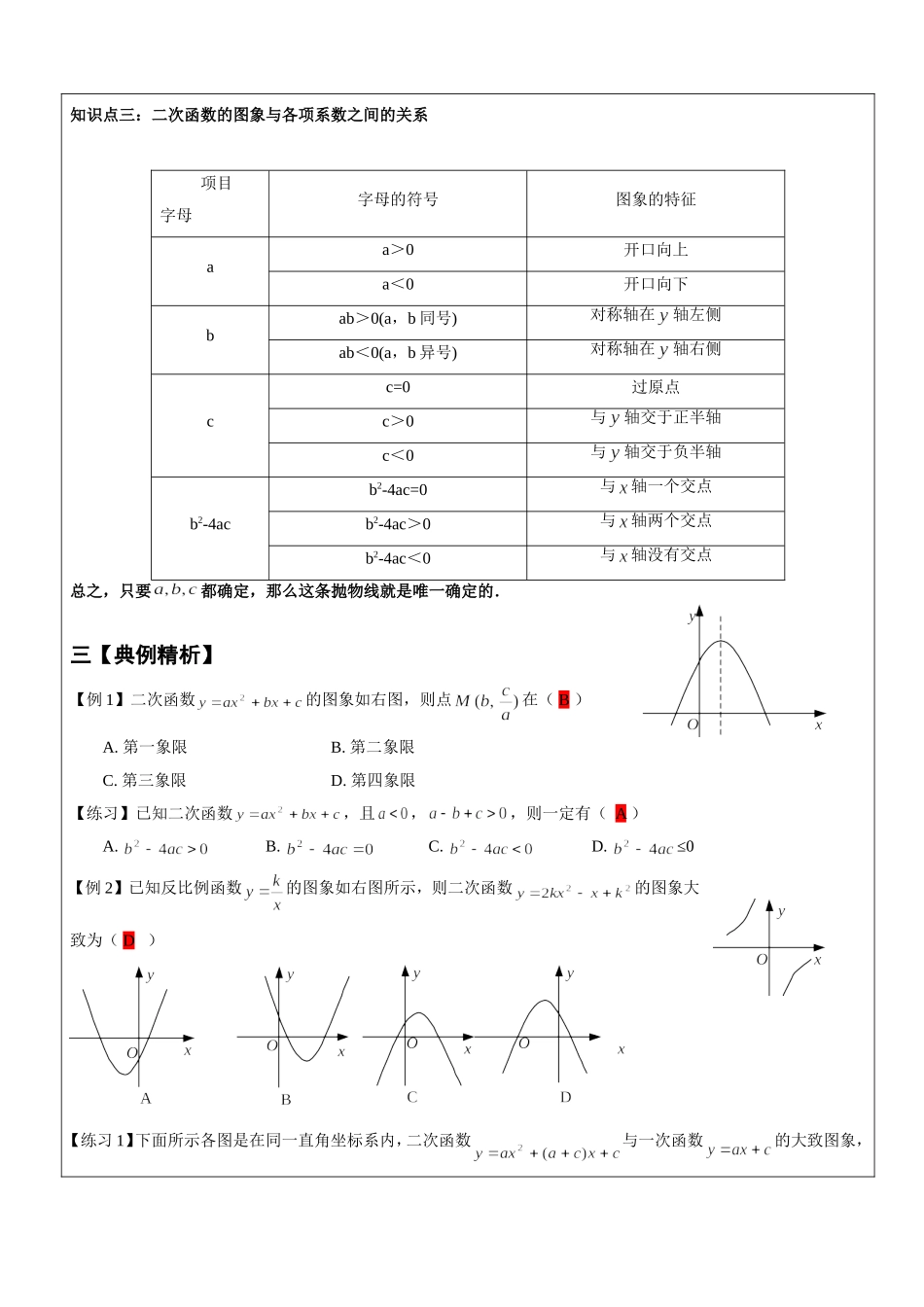
课题二次函数的图像与性质(五)教学目标1、会用描点法画二次函数2(0)yaxbxca的图象;2、会用配方法将二次函数2yaxbxc的解析式写成2()yaxhk的形式;3、通过图象能熟练地掌握二次函数2yaxbxc的性质;重点、难点1、运用二次函数的图象和性质解决简单的实际问题;2、深刻理解数学建模思想以及数形结合的思想.考点及考试要求二次函数的图像及性质教学内容一【课堂导入】问题1:对于二次函数(a≠0)的图象及图象的形状、开口方向、位置又是怎样的?启发:通过变形能否将转化为的形式?=由此可见:函数的图像与函数的图像的形状、开口方向均相同,只是位置不同,可以通过平移得到。抛物线的对称轴是直线,顶点坐标是()。当时,开口向上,顶点为最低点(最小值);当时,开口向下,顶点为最高点(最大值)。二【知识精讲】知识点一:二次函数图象的画法1.描点法(五点绘图法):步骤:1)利用配方法将二次函数化为顶点式;2)确定其开口方向、对称轴及顶点坐标;3)在对称轴两侧,左右对称地描点画图。2.平移法:步骤:1)利用配方法将二次函数化为顶点式确定其顶点为(h,k);2)作出的图像;3)将抛物线的图像平移,使其顶点平移到(h,k)。知识点二:二次函数的图像与性质函数二次函数2yaxbxc(a、b、c为常数,a≠0)图象0a0a开口方向向上向下对称轴直线直线顶点坐标(,)(,)增减性①当时,随的增大而减小;②当时,随的增大而增大;①当时,随的增大而增大;②当时,随的增大而减小;最大(小)值知识点三:二次函数的图象与各项系数之间的关系项目字母字母的符号图象的特征aa>0开口向上a<0开口向下bab>0(a,b同号)对称轴在轴左侧ab<0(a,b异号)对称轴在轴右侧cc=0过原点c>0与轴交于正半轴c<0与轴交于负半轴b2-4acb2-4ac=0与轴一个交点b2-4ac>0与轴两个交点b2-4ac<0与轴没有交点总之,只要都确定,那么这条抛物线就是唯一确定的.三【典例精析】【例1】二次函数的图象如右图,则点在(B)A.第一象限B.第二象限C.第三象限D.第四象限【练习】已知二次函数,且,,则一定有(A)A.B.C.D.≤0【例2】已知反比例函数的图象如右图所示,则二次函数的图象大致为(D)【练习1】下面所示各图是在同一直角坐标系内,二次函数与一次函数的大致图象,有且只有一个是正确的,正确的是(C)【练习2】已知:函数的图象如图:那么函数解析式为(A)A.B.C.D.【例3】已知:m,n是方程x2-6x+5=0的两个实数根,且m