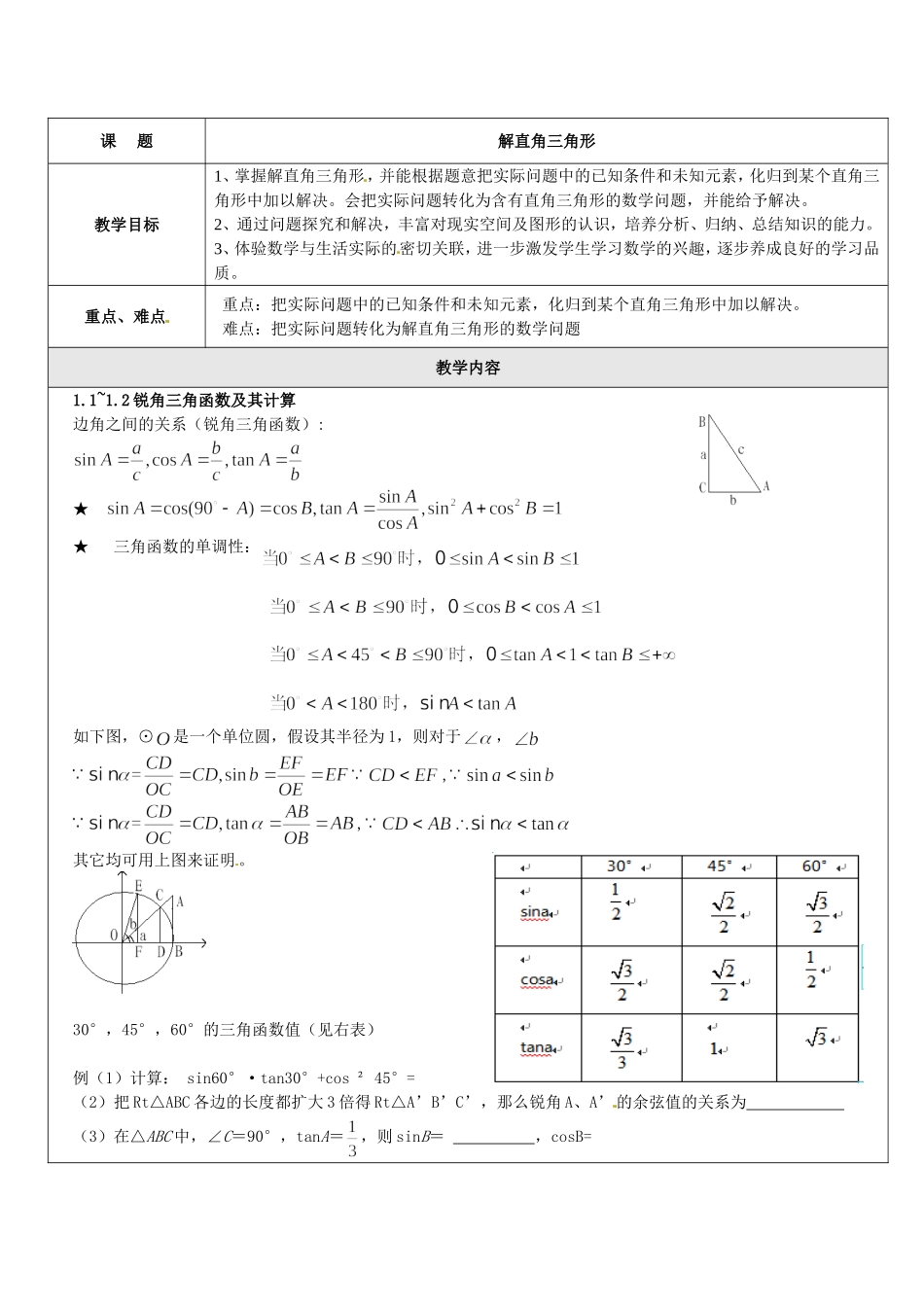
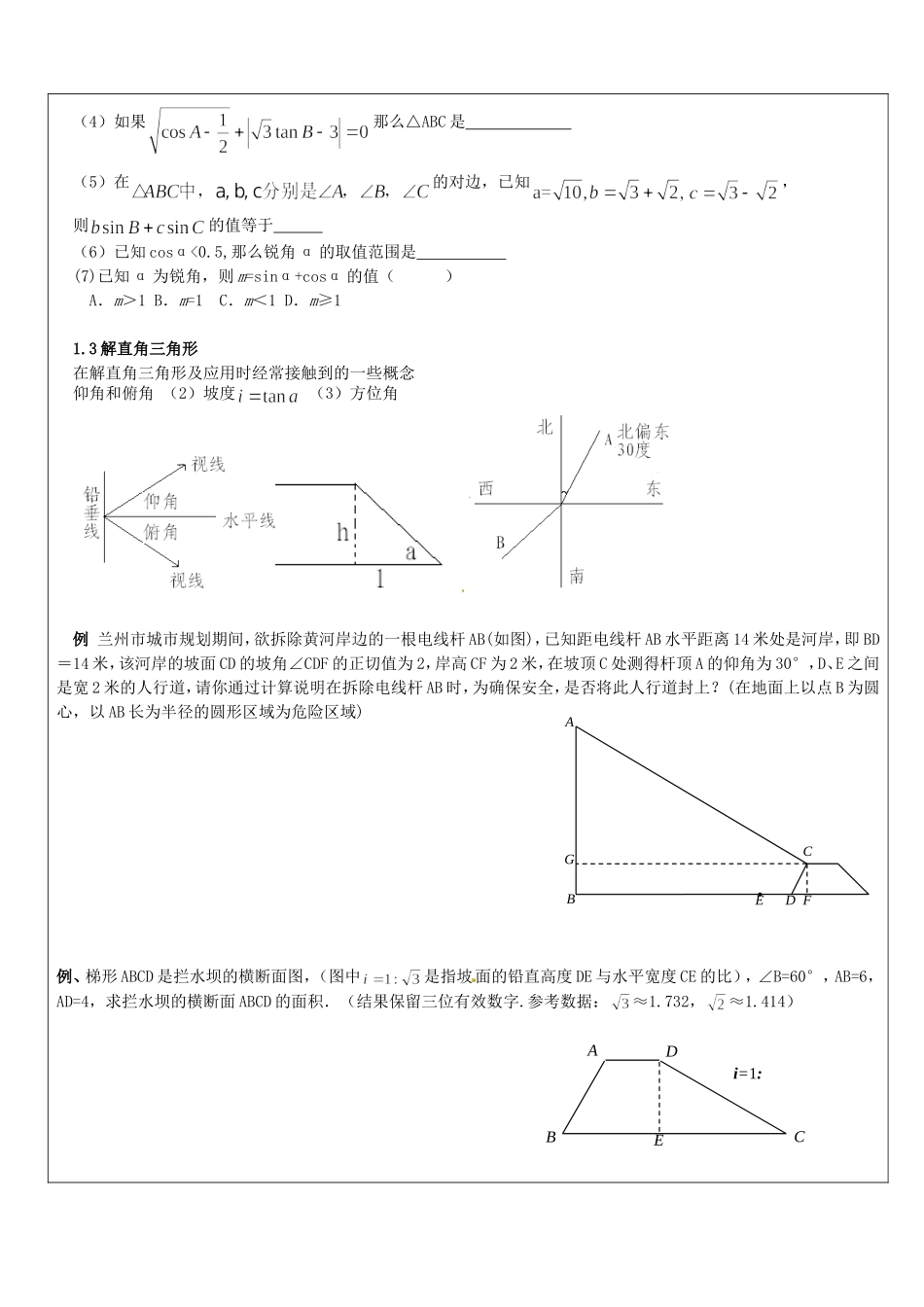
课题解直角三角形教学目标1、掌握解直角三角形,并能根据题意把实际问题中的已知条件和未知元素,化归到某个直角三角形中加以解决。会把实际问题转化为含有直角三角形的数学问题,并能给予解决。2、通过问题探究和解决,丰富对现实空间及图形的认识,培养分析、归纳、总结知识的能力。3、体验数学与生活实际的密切关联,进一步激发学生学习数学的兴趣,逐步养成良好的学习品质。重点、难点重点:把实际问题中的已知条件和未知元素,化归到某个直角三角形中加以解决。难点:把实际问题转化为解直角三角形的数学问题教学内容1.1~1.2锐角三角函数及其计算边角之间的关系(锐角三角函数):★★三角函数的单调性:如下图,⊙是一个单位圆,假设其半径为1,则对于,,,其它均可用上图来证明。30°,45°,60°的三角函数值(见右表)例(1)计算:sin60°·tan30°+cos²45°=(2)把Rt△ABC各边的长度都扩大3倍得Rt△A’B’C’,那么锐角A、A’的余弦值的关系为(3)在△ABC中,∠C=90°,tanA=,则sinB=,cosB=ADBEi=1:C(4)如果那么△ABC是(5)在的对边,已知,则的值等于(6)已知cosα<0.5,那么锐角α的取值范围是(7)已知α为锐角,则m=sinα+cosα的值()A.m>1B.m=1C.m<1D.m≥11.3解直角三角形在解直角三角形及应用时经常接触到的一些概念仰角和俯角(2)坡度(3)方位角例兰州市城市规划期间,欲拆除黄河岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)例、梯形ABCD是拦水坝的横断面图,(图中是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果保留三位有效数字.参考数据:≈1.732,≈1.414)CBADEFG例、如图,一条小船从港口出发,沿北偏东方向航行海里后到达处,然后又沿北偏西方向航行海里后到达处.问此时小船距港口多少海里?(结果精确到1海里),,,.例、如图所示,A、B两地之间有一条河,原来从A地到B地需要经过DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.一直BC=11km,∠A=45°,∠B=37°.桥DC和AB平行,则现在从A地到达B地可比原来少走多少路程?(结果精确到0...