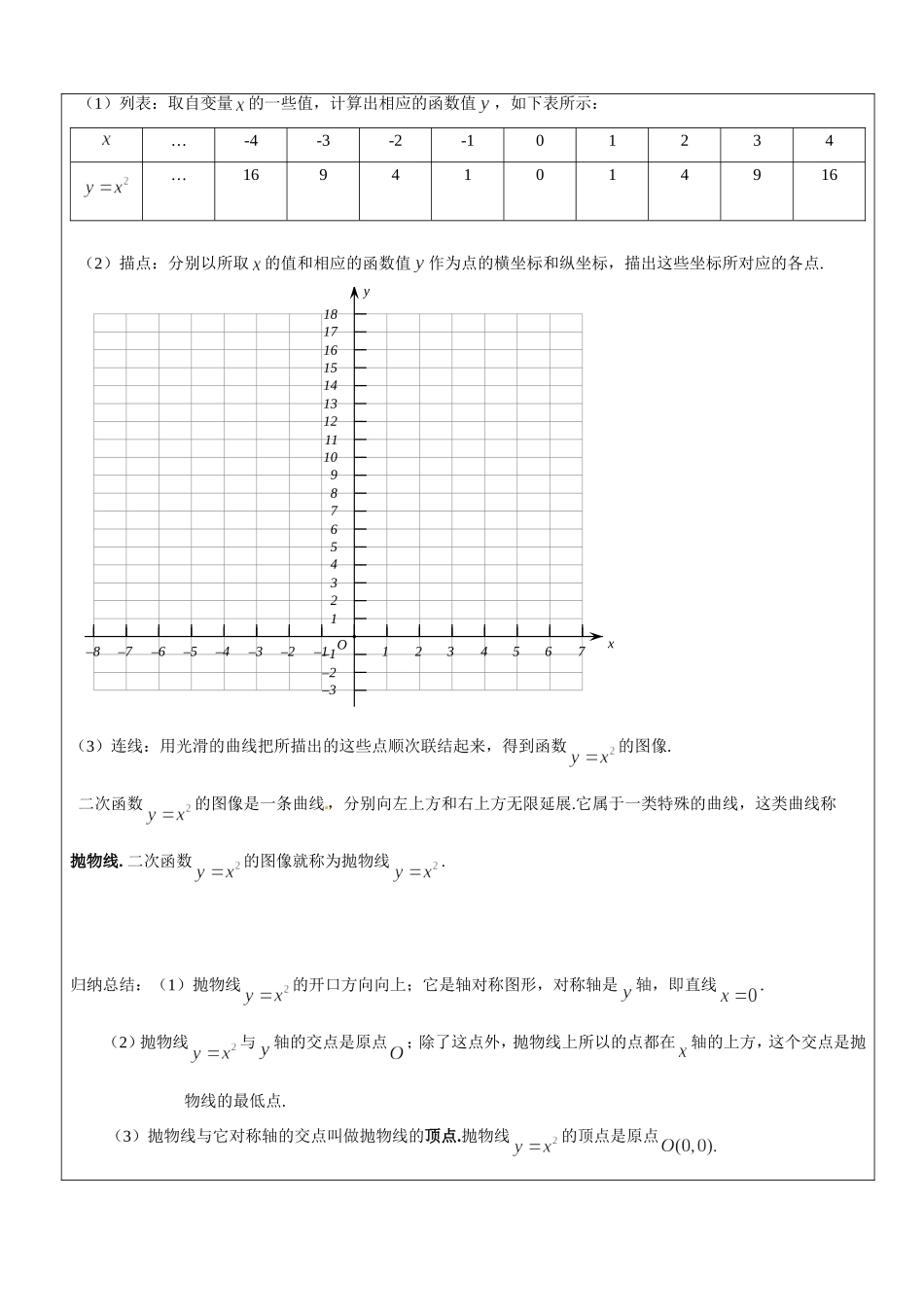
课题二次函数的图像与性质(一)教学目标1.知道二次函数的概念及一般表达式;2.会利用二次函数的概念分析解题;3.列二次函数表达式解实际问题.重点、难点1.二次函数的概念;2.理由二次函数解决实际问题考点及考试要求二次函数图像的描绘和图像特征的归纳教学内容一【课堂导入】1、正比例函数、一次函数的图象是直线,反比例函数的图象是双曲线,用描点法画图象有哪些步骤?(列表、描点、画图)2、一次函数的性质有哪些?3、我们已经知道了二次函数的一般形式是.二【知识精讲】知识点1:二次函数的图像1、对于二次函数(其中是常数,且)图像的研究,就从特殊形式的二次函数开始.操作:在平面直角坐标系xOy中,按照下列步骤画二次函数的图像.(1)列表:取自变量的一些值,计算出相应的函数值,如下表所示:…-4-3-2-101234…16941014916(2)描点:分别以所取的值和相应的函数值作为点的横坐标和纵坐标,描出这些坐标所对应的各点.yOx–1–2–3–4–5–6–7–81234567123456789101112131415161718–1–2–3(3)连线:用光滑的曲线把所描出的这些点顺次联结起来,得到函数的图像.二次函数的图像是一条曲线,分别向左上方和右上方无限延展.它属于一类特殊的曲线,这类曲线称抛物线.二次函数的图像就称为抛物线.归纳总结:(1)抛物线的开口方向向上;它是轴对称图形,对称轴是轴,即直线.(2)抛物线与轴的交点是原点;除了这点外,抛物线上所以的点都在轴的上方,这个交点是抛物线的最低点.(3)抛物线与它对称轴的交点叫做抛物线的顶点.抛物线的顶点是原点例1、在同一直角坐标系中.(1)画出下列函数的图像;①②③④(2)说出四个函数图像的区别与联系.解:(1)①列表:…-4-3-2-101234……84.520.500.524.58……-8-4.5-2-0.50-0.5-2-4.5-8……-2-1.5-1-0.500.511.52……84.520.500.524.58……-8-4.5-2-0.50-0.5-2-4.5-8…②描点③连线(2)四个函数的区别于联系如下表:yOx2468-2-4-6-8-8-6-4-28642【练习】在同一直角坐标系中,用描点法画出下列函数的图像:①;②;③(1)列表:x…-2-1012……41014……-4-10-1-4……-8-20-2-8…(2)指出它们的对称轴、顶点、开口方向,并指出开口最小的抛物线2、二次函数的图像的性质函数区别联系图像开口方向抛物线位置开口大小四个图像的顶点都是原点,对称轴都是轴.开口向上抛物线除顶点在轴上外,其余在轴上方,并向上无限延伸.当变大时,抛物线开口变窄;当变小时,抛物线开口变宽.开口向下抛物线除顶点...