16.1 第2课时 二次根式的性质.pptxVIP免费

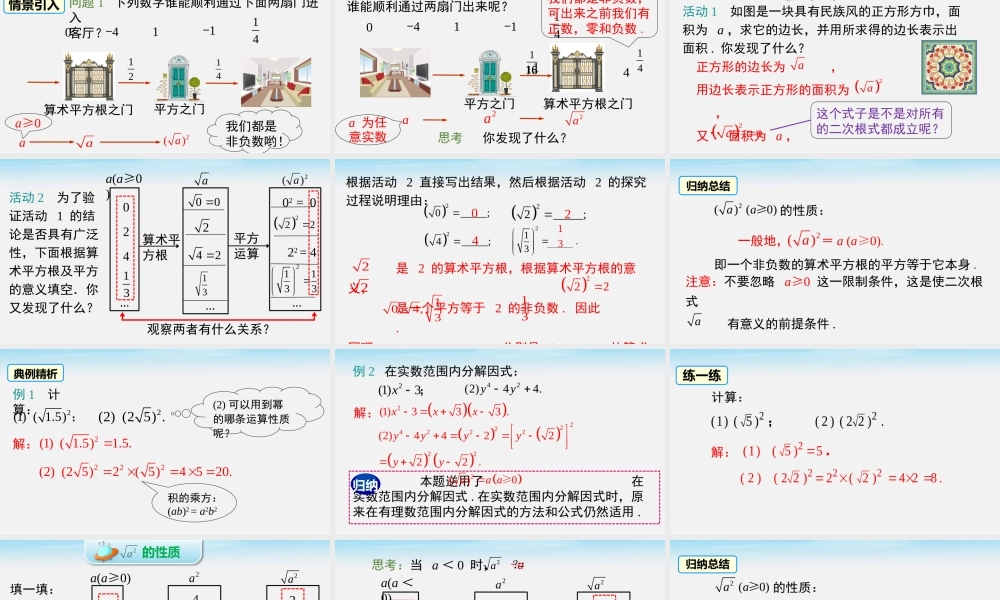
16.1二次根式第2课时二次根式的性质第16章二次根式导入新课情景引入问题1下列数字谁能顺利通过下面两扇门进入客厅？算术平方根之门平方之门a2()aaa≥0我们都是非负数哟！140-4-111214问题2若下列数字想从客厅出来，谁能顺利通过两扇门出来呢？算术平方根之门平方之门2a2aaa为任意实数思考你发现了什么？140-4-11164111614我们都是非负数，可出来之前我们有正数，零和负数.新课讲授正方形的边长为，用边长表示正方形的面积为，又 面积为a，活动1如图是一块具有民族风的正方形方巾，面积为a，求它的边长，并用所求得的边长表示出面积.你发现了什么？a2aa2a这个式子是不是对所有的二次根式都成立呢？2()a（a≥0）的性质活动2为了验证活动1的结论是否具有广泛性，下面根据算术平方根及平方的意义填空．你又发现了什么？...算术平方根平方运算024...004213a(a≥0)a2)(a02=0...1321133观察两者有什么关系？222=42222_________1.322_____;24_____;20_____;41320根据活动2直接写出结果，然后根据活动2的探究过程说明理由：是2的算术平方根，根据算术平方根的意义，是一个平方等于2的非负数.因此.同理分别是0的算术2222210,4,313归纳总结的性质：2()(0)aa≥一般地，＝a(a≥0).2()a即一个非负数的算术平方根的平方等于它本身.注意：不要忽略a≥0这一限制条件，这是使二次根式有意义的前提条件.a典例精析例1计算：2(1)(1.5)；2(2)(25).解：2(1)(1.5)1.5.222(2)(25)2(5)4520.(2)可以用到幂的哪条运算性质呢？积的乘方：(ab)2=a2b2例2在实数范围内分解因式：42(2)44.yy解：222422222(2)442222.yyyyyy2(1)3x；2(1)333.xxx本题逆用了在实数范围内分解因式.在实数范围内分解因式时，原来在有理数范围内分解因式的方法和公式仍然适用.归纳2()0aaa≥练一练计算：22(1)(5)(2)(22).；解：2(1)(5)5.222(2)(22)2(2)428....平方运算算术平方根20.10...449a(a≥0)2a2a2...23观察两者有什么关系？0.010.102302a填一填：＝a(a≥0)2a的性质...平方运算算术平方根-2-0.1...4492a2a2...23观察两者有什么关系？0.010.123a(a＜0)思考：当a＜0时，=2a？-a归纳总结a(a≥0)2aa-a(a＜0)即任意一个数的平方的算术平方根等于原数的绝对值.的性质：2(0)aa≥例3化简：(1)16；2(2)(5)；解...