沪教版(五四学制)七上：9.16 分组分解法 课件（17张ppt）.pptVIP免费

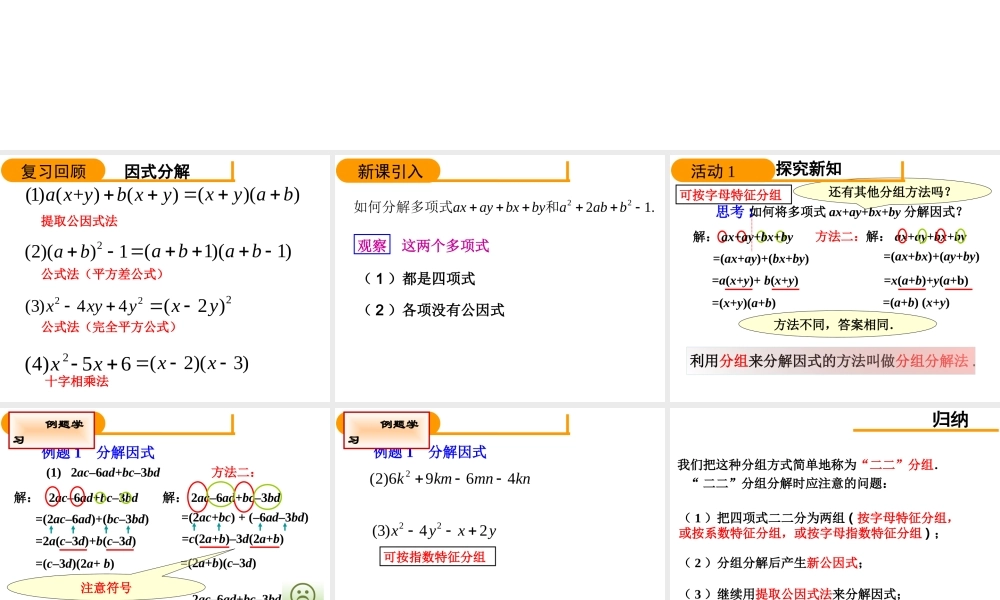
因式分解(1)(+)()axybxy2(2)()1ab22(3)44xxyy公式法（平方差公式）公式法（完全平方公式）2(4)56xx十字相乘法提取公因式法(1)(1)abab2(2)xy(2)(3)xx()()xyab复习回顾新课引入2221.axaybxbyaabb如何分解多项式和观察这两个多项式（1）都是四项式（2）各项没有公因式思考:如何将多项式ax+ay+bx+by分解因式？解：ax+ay+bx+by=(ax+ay)+(bx+by)=a(x+y)+b(x+y)=(x+y)(a+b)方法二：解：ax+ay+bx+by=(ax+bx)+(ay+by)=x(a+b)+y(a+b)=(a+b)(x+y)还有其他分组方法吗？方法不同，答案相同．探究新知活动1利用分组来分解因式的方法叫做分组分解法.可按字母特征分组例题1分解因式(1)2ac–6ad+bc–3bd解：2ac–6ad+bc–3bd=(2ac–6ad)+(bc–3bd)=2a(c–3d)+b(c–3d)=(c–3d)(2a+b)方法二：解：2ac–6ad+bc–3bd=(2ac+bc)+(–6ad–3bd)=c(2a+b)–3d(2a+b)=(2a+b)(c–3d)2ac–6ad+bc–3bd=(2ac–3bd)+(–6ad+bc)可按系数特征分组注意符号例题学习2(2)6964kkmmnkn例题1分解因式例题学习22(3)42xyxy可按指数特征分组归纳“二二”分组分解时应注意的问题：（1）把四项式二二分为两组(按字母特征分组，或按系数特征分组，或按字母指数特征分组)；（2）分组分解后产生新公因式；（3）继续用提取公因式法来分解因式；（4）分解到不能分解为止．我们把这种分组方式简单地称为“二二”分组．例题2分解因式2x3–2x2y+8y–8x解：2x3–2x2y+8y–8x=2[(x3–x2y)+(4y–4x)]=2[x2(x–y)–4(x–y)]=2(x–y)(x2–4)有公因式的先提取公因式=2(x–y)(x+2)(x–2)（1）分解因式时先观察，有公因式的应先提取公因式；（2）分解到不能分解为止．还能继续分解吗？=2(x3–x2y+4y–4x)例题学习分解因式：课堂练习课堂练习2232(1)22(2)33(3)2918aababxyxyxxxyxy分解因式：探究新知活动2a2+2ab+b2–1.分析:用“二二”分组能分解吗？多项式有何特征?完全平方式(a+b)2–1整体平方差公式解：a2+2ab+b2–1=(a2+2ab+b2)–1这种分组方法称为“一三”分组．=(a+b)2–1=(a+b+1)(a+b–1)例题3分解因式：x2–4x–y2+4；分析:如何分组？多项式有何特征?(x2–4x+4)–y2(x–2)2–y2解：(1)x2–4x–y2+4=(x2–4x+4)–y2=(x–2)2–y2=(x–2+y)(x–2–y)“一三”分组1.含三项的这组是完全平方式；（平方项同号）2.先用完全平方公式，再用平方差公式．“一三”分组的要点:例题学习完全平方公式平方差公式请找出下列多项式中...