北京课改初中数学九上《21.2 30°、45°、60°角的三角函数值》PPT课件 (3).pptVIP免费

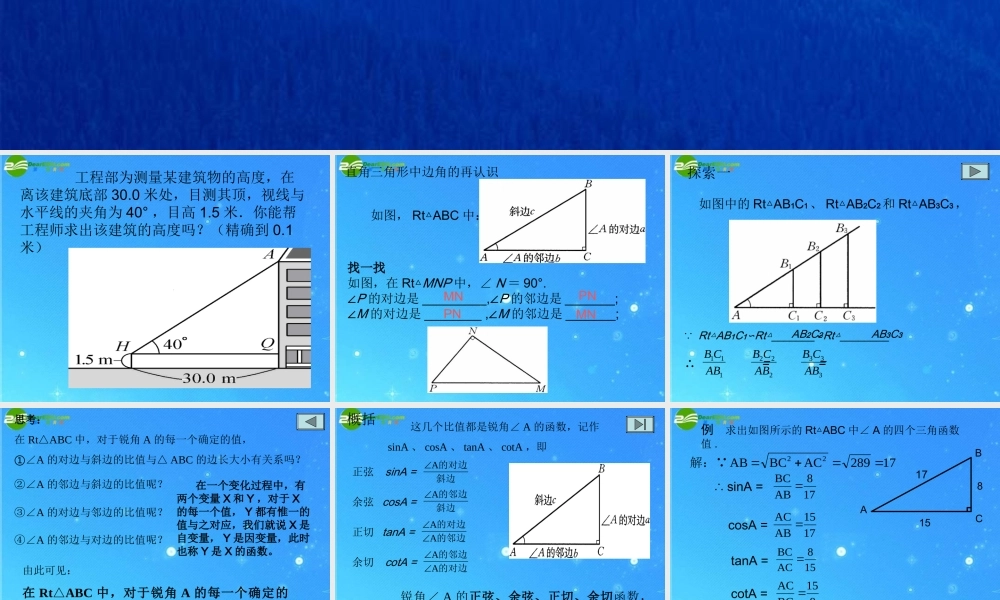
21.2锐角的三角函数值工程部为测量某建筑物的高度，在离该建筑底部30.0米处，目测其顶，视线与水平线的夹角为40°，目高1.5米．你能帮工程师求出该建筑的高度吗？（精确到0.1米）直角三角形中边角的再认识如图，RtABC△中：找一找如图，在Rt△MNP中，∠N＝90°.∠P的对边是_________,∠P的邻边是_______;∠M的对边是________,∠M的邻边是_______;MNPNPNMN如图中的RtAB△1C1、RtAB△2C2和RtAB△3C3， RtAB△1C1Rt_______Rt________∽△∽△∴==111ABCBAB3C3AB2C2333ABCB222ABCB探索一思考：在Rt△ABC中，对于锐角A的每一个确定的值，①∠A的对边与斜边的比值与△ABC的边长大小有关系吗？②∠A的邻边与斜边的比值呢？③∠A的对边与邻边的比值呢？④∠A的邻边与对边的比值呢？由此可见：在Rt△ABC中，对于锐角A的每一个确定的值，其对边与斜边、邻边与斜边、对边与邻边、邻边与对边的比值是惟一确定的.在一个变化过程中，有两个变量X和Y，对于X的每一个值，Y都有惟一的值与之对应，我们就说X是自变量，Y是因变量，此时也称Y是X的函数。这几个比值都是锐角∠A的函数，记作sinA、cosA、tanA、cotA，即sinA=斜边的对边AcosA=斜边的邻边A的对边的邻边AA的邻边的对边AAtanA=cotA=锐角∠A的正弦、余弦、正切、余切函数，统称为锐角∠A的三角函数.概括正弦余弦正切余切例求出如图所示的RtABC△中∠A的四个三角函数值.158CBA17289ACBCAB22解： ∴sinA=178ABBCcosA=tanA=cotA=1715ABAC158ACBC815BCAC17求出如图所示的Rt△DEC（∠E＝90°）中∠D的四个三角函数值.牛刀小试解： 864EDCDCE22∴sinD=54CDCEcosD=tanD=cotD=53CDED34EDCE43CEED8探索二（1）根据三角函数的定义，sin30°是一个常数.用刻度尺量出你所用的含30°的三角尺中，30°所对的直角边与斜边的长，与同桌交流，看看这个常数是什么.sin30°=21＝斜边对边即斜边等于对边的2倍.因此我们还可以得到：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.30BCA∴BC=21 ∠C=90°,A=30°∠AB（直角三角形中30°角所对的直角边等于斜边的一半）几何论证(1)DBCA(2)DCBA（2）根据sin30°=，怎样求cos30°、tan30°、cot30°的值呢？216030321CBAcos30°=tan30°=cot30°=sin60°=cos60°=tan60°=cot60°=（3）2331=3313=32321333(4)用类似的方法求sin45°、cos45°、tan45°、cot45°的值，并完成课本P109的表格。21145CBAs...