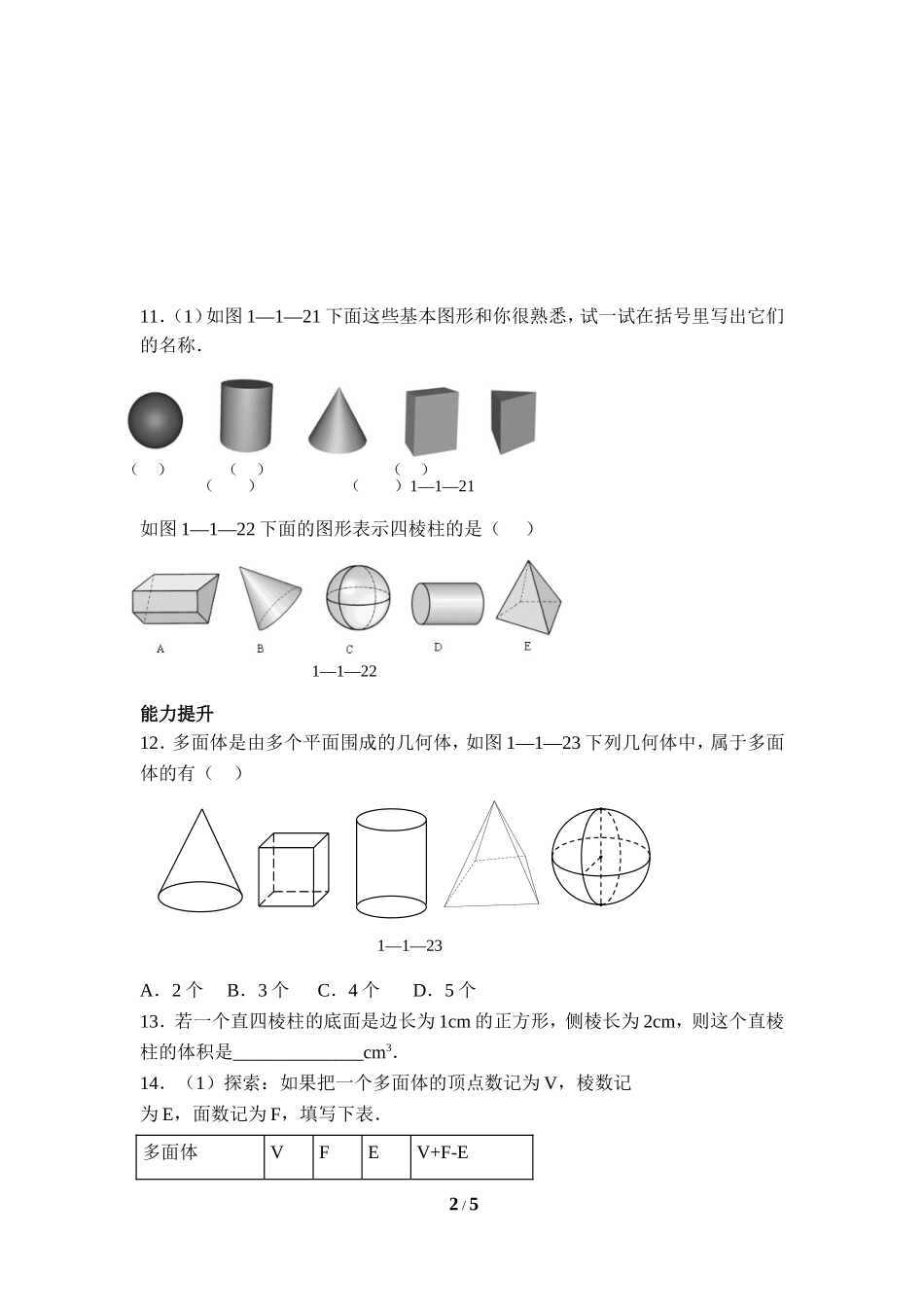
生活中的立体图形新题精炼基础巩固1.如图1—1—17观察下列实物模型,其形状是圆柱体的是()2.下列图形中不是立体图形的是()A.圆锥B.圆柱C.圆D.球3.如图1—1—18是一个生日蛋糕盒,这个盒子有几条棱()A.6条B.12条C.18条D.24条4.下列立体图形中,有五个面的是()A.四棱锥B.五棱锥C.四棱柱D.五棱柱5.将下面的直角梯形绕直线l旋转一周,可以得到如图1—1—19立体图形的是()6.汽车的雨刷把玻璃上的雨水刷干净属于的实际应用是()A.点动成线B.线动成面C.面动成体D.以上都不对7.若一个棱柱的底面是一个七边形,则它的侧面必须有_____个长方形,它一共有_____个面,______个顶点.8.一个棱柱有18条棱,那么它的底面一定是______边形.9.六棱柱有_____个顶点,有_______条侧棱.10.如图1—1—20至少找出下列几何体的4个共同点.1/5A.B.C.D.1—1—17A.B.C.D.1—1—201—1—191—1—1811.(1)如图1—1—21下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称.(2)将这些几何体分类,并写出分类的理由.如图1—1—22下面的图形表示四棱柱的是()能力提升12.多面体是由多个平面围成的几何体,如图1—1—23下列几何体中,属于多面体的有()A.2个B.3个C.4个D.5个13.若一个直四棱柱的底面是边长为1cm的正方形,侧棱长为2cm,则这个直棱柱的体积是______________cm3.14.(1)探索:如果把一个多面体的顶点数记为V,棱数记为E,面数记为F,填写下表.多面体VFEV+F-E2/5()()()()()1—1—211—1—231—1—22四面体长方体五棱柱(2)猜想:由上面的探究你能得到一个什么结论?(3)验证:再找出一个多面体,数一数它有几个顶点,几条棱,几个面,看看面数、顶点数、棱数是否满足上述关系.(4)应用(2)的结论对所有的多面体都成立,伟大的数学家欧拉证明了这个关系式,上述关系式叫做欧拉公式.根据欧拉公式,想一想会不会有一个多面体,它有10个面,30条棱,20个顶点?新题精炼答案基础巩固1.D思路导引:圆柱的上下底面都是圆,所以正确的是D.2.C思路导引:圆是平面图形3.C思路导引:观察图形可知上下面的棱数都是6,侧面的棱数是6.则这个盒子的棱数为:6+6+6=18.4.A思路导引:要明确棱柱和棱锥的组成情况,棱柱有两个底面,棱锥有一个底面.5.B面动成体.由题目中的图示可知:此几何体是直角梯形转成圆台的条件是:3/5绕垂直于底的腰旋转.6.B思路导引:汽汽车的雨刷实际上是一条线,通过...