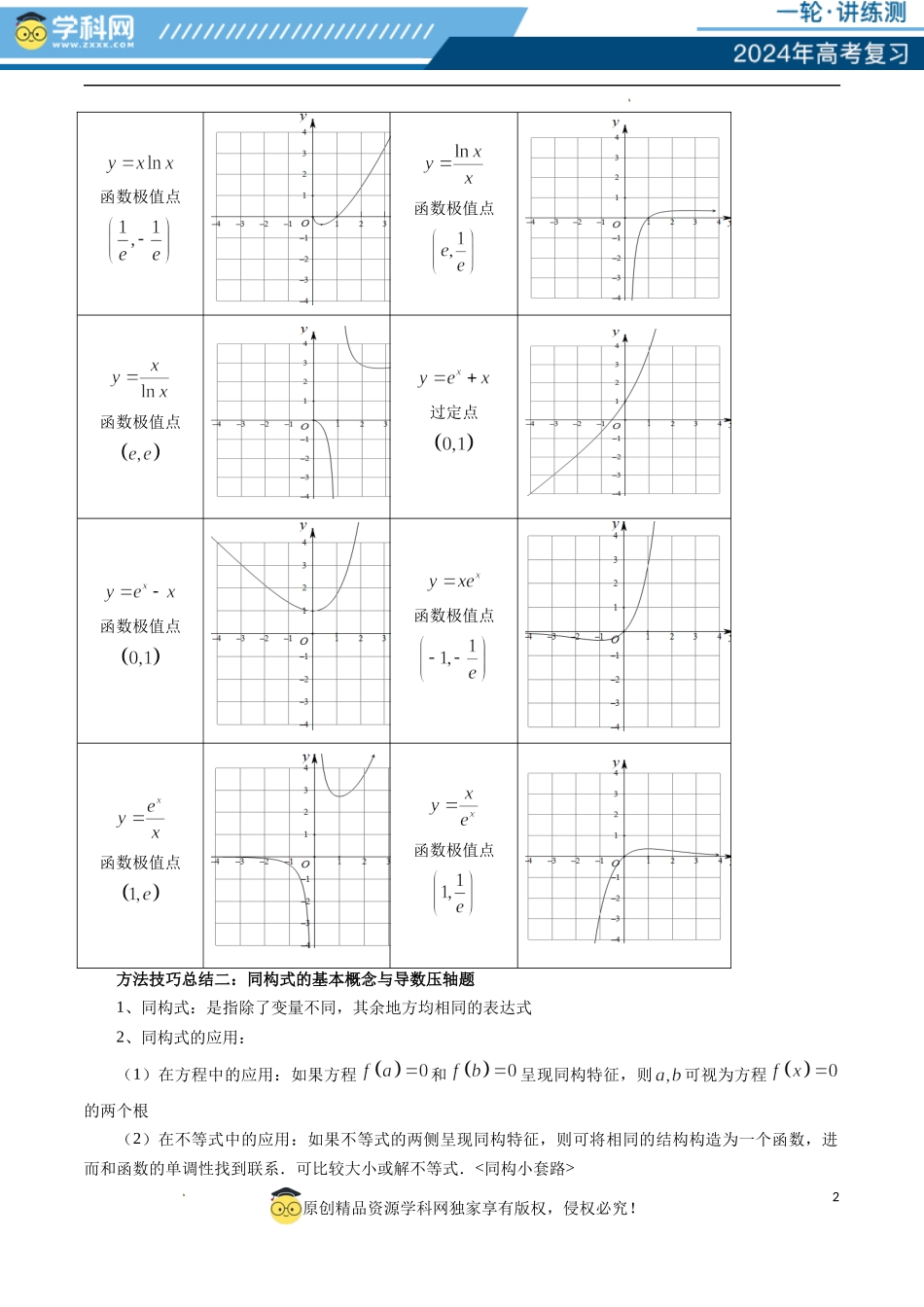
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司重难点突破11导数中的同构问题目录方法技巧总结一、常见的同构函数图像函数表达式图像函数表达式图像函数极值点2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司函数极值点函数极值点函数极值点过定点函数极值点函数极值点函数极值点函数极值点方法技巧总结二:同构式的基本概念与导数压轴题1、同构式:是指除了变量不同,其余地方均相同的表达式2、同构式的应用:(1)在方程中的应用:如果方程和呈现同构特征,则可视为方程的两个根(2)在不等式中的应用:如果不等式的两侧呈现同构特征,则可将相同的结构构造为一个函数,进而和函数的单调性找到联系.可比较大小或解不等式.<同构小套路>3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司①指对各一边,参数是关键;②常用“母函数”:,;寻找“亲戚函数”是关键;③信手拈来凑同构,凑常数、、参数;④复合函数(亲戚函数)比大小,利用单调性求参数范围.(3)在解析几何中的应用:如果满足的方程为同构式,则为方程所表示曲线上的两点.特别的,若满足的方程是直线方程,则该方程即为直线的方程(4)在数列中的应用:可将递推公式变形为“依序同构”的特征,即关于与的同构式,从而将同构式设为辅助数列便于求解3、常见的指数放缩:ex≥x+1(x=0);ex≥ex(x=1)4、常见的对数放缩:1−1x≤lnx≤x−1(x=1);lnx≤xe(x=e)5、常见三角函数的放缩:x∈(0,π2),sinx