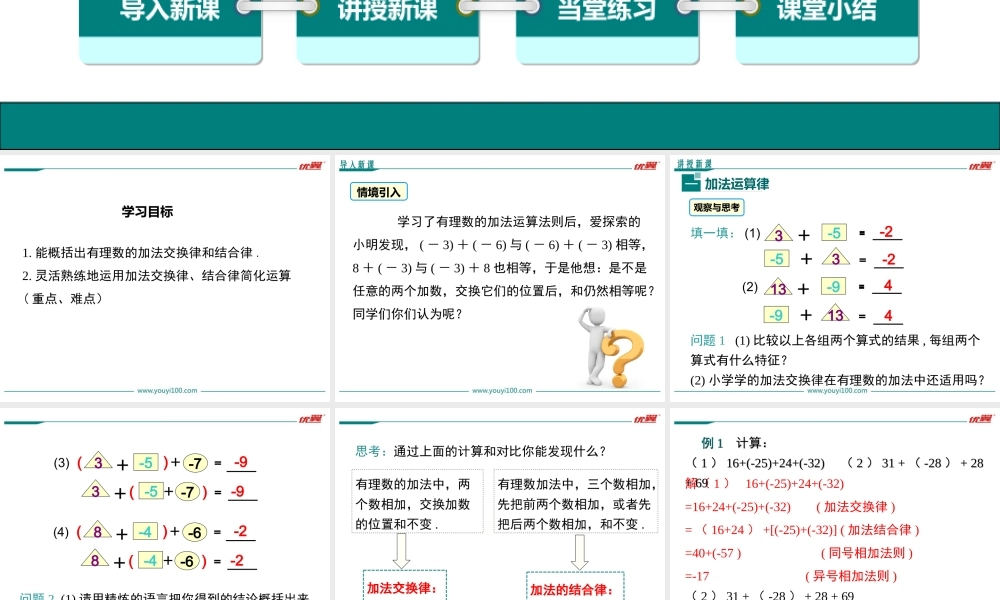
1.4有理数的加法和减法第1章有理数导入新课讲授新课当堂练习课堂小结七年级数学上(XJ)教学课件1.4.1有理数加法第2课时有理数加法的运算律学习目标1.能概括出有理数的加法交换律和结合律.2.灵活熟练地运用加法交换律、结合律简化运算(重点、难点)导入新课情境引入学习了有理数的加法运算法则后,爱探索的小明发现,(-3)+(-6)与(-6)+(-3)相等,8+(-3)与(-3)+8也相等,于是他想:是不是任意的两个加数,交换它们的位置后,和仍然相等呢?同学们你们认为呢?3﹢-5﹦__-2-53﹢﹦__-2讲授新课加法运算律一观察与思考填一填:(1)问题1(1)比较以上各组两个算式的结果,每组两个算式有什么特征?(2)小学学的加法交换律在有理数的加法中还适用吗?13﹢-9﹦__4-913﹢﹦__4(2)3-5﹢﹦__)-7-9(﹢3-5﹢﹢﹦__-7-9()(3)8-4﹢﹦__)-6-2(﹢8-4﹢﹢﹦__-6-2()(4)问题2(1)请用精炼的语言把你得到的结论概括出来.(2)你能用字母把这个规律表示出来吗?有理数的加法中,两个数相加,交换加数的位置和不变.加法交换律:a+b=b+a有理数加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.加法的结合律:(a+b)+c=a+(b+c)思考:通过上面的计算和对比你能发现什么?解(1)16+(-25)+24+(-32)=16+24+(-25)+(-32)(加法交换律)=(16+24)+[(-25)+(-32)](加法结合律)=40+(-57)(同号相加法则)=-17(异号相加法则)例例11计算:计算:((11))16+(-25)+24+(-32)16+(-25)+24+(-32)((22))31+31+((-28-28))+28+28+69+69(2)31+(-28)+28+69=31+69+[(-28)+28](加法交换律和结合律)=100+0=100例2计算:(1)(-32)+7+(-8);(2)4.37+(-8)+(-4.37);(3)22355()4(2).5757解:(32)7(8)(32)(8)7[(32)(8)]7(40)733;(1)4.37(8)(4.37)4.37(4.37)(8)[4.37(4.37)](8)0(8)8;(2)22355()4(2)5757232554()(2)55772325(54)[()(2)]557710(3)7.(3)(3)22355()4(2).5757常用的三个规律:1.有相反数的可先把相反数相加,能凑整的可先凑整;2.有分母相同的,可先把分母相同的数结合相加;3.然后把正数或负数分别结合在一起相加.小组讨论:你是抓住数的什么特点使计算简化的?依据是什么?(1)(-2.48)+4.33+(-7.52)+(-4.33)(2)例3计算:解:原式=[(-2.48)+(-7.52)]+[(+4.33)+(-4.33)]=...