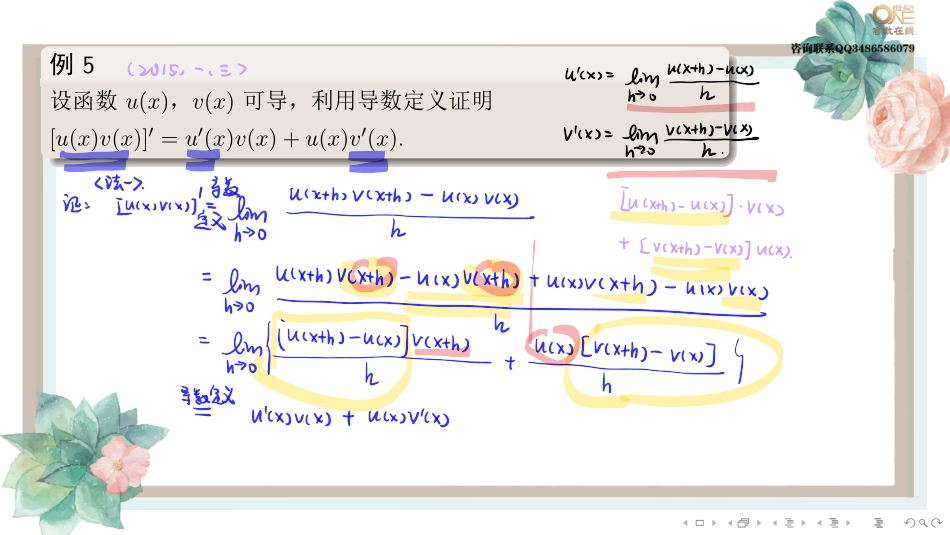
........第二节导数与微分的计算常数和基本初等函数的导数公式(1)(C)′=0,(2)(xµ)′=µxµ−1,(3)(sinx)′=cosx,(4)(cosx)′=−sinx,(5)(tanx)′=sec2x,(6)(cotx)′=−csc2x,(7)(secx)′=secxtanx,(8)(cscx)′=−cscxcotx,(9)(ax)′=axlna(a>0,a̸=1),(10)(ex)′=ex,(11)(logax)′=1xlna(a>0,a̸=1),(12)(lnx)′=1x,(13)(arcsinx)′=1√1−x2,(14)(arccosx)′=−1√1−x2,(15)(arctanx)′=11+x2,(16)(arccotx)′=−11+x2........函数的和、差、积、商的求导法则设u=u(x),v=v(x)都可导,则(1)(u±v)′=u′±v′,(2)(Cu)′=Cu′(C是常数),(3)(uv)′=u′v+uv′,(4)(uv)′=u′v−uv′v2(v̸=0).链式法则若u=g(x)在点x可导,而y=f(u)在点u=g(x)可导,则复合函数y=f(g(x))在点x可导,且其导数为dydx=f′(u)·g′(x),或dydx=dydu·dudx.........例5..设函数u(x),v(x)可导,利用导数定义证明[u(x)v(x)]′=u′(x)v(x)+u(x)v′(x)........思考利用导数定义证明(uv)′=u′v−uv′v2(v̸=0)........微分的计算dy=f′(x)dx.函数的和、差、积、商的微分法则(1)d(u±v)=du±dv,(2)d(Cu)=Cdu(C是常数),(3)d(uv)=vdu+udv,(4)d(uv)=vdu−udvv2(v̸=0).........例6..计算下列函数的导数.(1)y=arcsinex.(2)y=1+sinx1+cosx.(3)y=1√1−x2.(4)f(x)可导,y=f(sin2x)+f(cos2x)................例7..设函数g(x)可微,h(x)=e1+g(x),h′(1)=1,g′(1)=2,则g(1)等于()(A)ln3−1.(B)−ln3−1.(C)−ln2−1.(D)ln2−1........求一元隐函数y(x)的导数的方法对已知方程两端同时关于x求导或者同时微分..例8..已知函数y=y(x)由方程ey+6xy+x2−1=0确定,则y′′(0)=........反函数的求导法则若函数y=f(x)在区间Ix内单调、可导且f′(x)̸=0,则它的反函数x=f−1(y)在区间Iy={y|y=f(x),x∈Ix}内也可导,并且[f−1(y)]′=1f′(x)或dxdy=1dydx.........例9..设y=x+sinx,求d2xdy2........求由参数方程确定的函数的一阶、二阶导数(数三不要求)若函数由参数方程{x=φ(t),y=ψ(t)确定,φ(t),ψ(t)均二阶可导,且φ′(t)̸=0,则dydx=dydt/dxdt=ψ′(t)φ′(t),d2ydx2=ddx(dydx)=d(dydx)dt/dxdt.........例10..设x=t2+2t,y=ln(t+1),则d2ydx2=........高阶导数的计算利用求导法则逐次求导,在逐次求导的过程中寻找表达式的规律,进而归纳得出高阶导数的表达式.利用莱布尼茨公式.莱布尼茨公式若f=uv,则f(n)=(uv)(n)=n∑k=0Cknu(n−k)v(k).利用函数的泰勒级数.函数f(x)在x=x0处的泰勒级数∞∑n=0f(n)(x0)n!(x−x0)n中,(x−x0)n的系数为f(n)(x0)n!.........例11..求函数f(x)=x2ln(1+x)在x=0处的n阶导数f(n)(0)(n≥3)........����见讲义第二节同步习题.