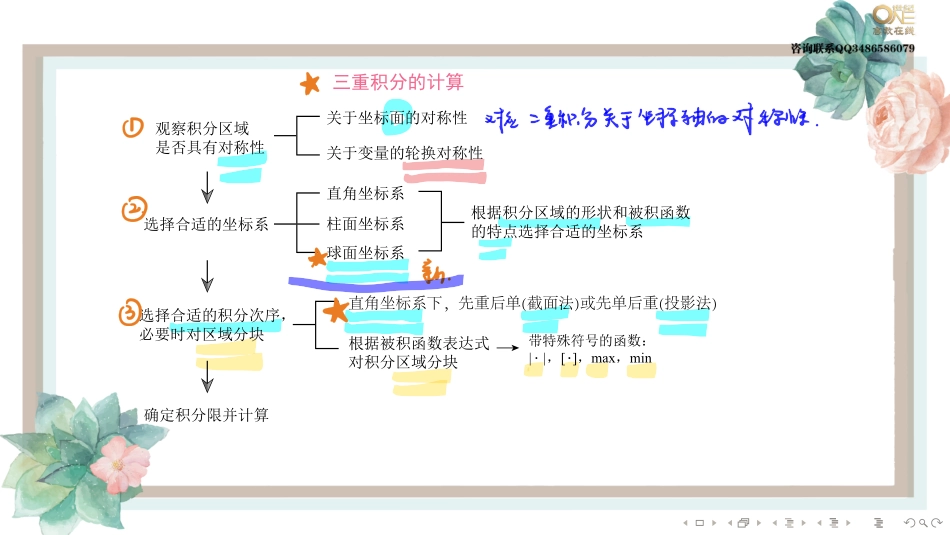
........第三节三重积分三重积分的定义与性质三重积分的中值定理设函数f(x,y,z)在闭区域Ω上连续,V是Ω的体积,则Ω上至少存在一点(ξ,η,ζ),使得˚Ωf(x,y,z)dv=f(ξ,η,ζ)V........�����������������������������������������������������������������������������������直角坐标系下,先重后单(截面法)或先单后重(投影法)�������������������������||�[]�max�min������������������������������.......三重积分中的轮换对称性三重积分中的轮换对称性指的是,轮换坐标轴(x轴,y轴,z轴),积分区域Ω的表示不变.此时,相应地轮换被积函数中的x,y,z的位置,积分值不变.设f(x,y,z)是有界闭区域Ω上的连续函数.若积分区域Ω对变量x,y,z具有轮换对称性,则˚Ωf(x,y,z)dv=˚Ωf(y,z,x)dv=˚Ωf(z,x,y)dv=13˚Ω[f(x,y,z)+f(y,z,x)+f(z,x,y)]dv........常见的具有轮换对称性的空间区域(a)(b)xyz(c)OxyzO(d)111111zyxzyxOOOORRRRRR.......在直角坐标系下计算三重积分.1先单后重..2先重后单.xbaΩy=y2(x)y=y1(x)z=z2(x,y)yzz1z2S2S1Dxy(x,y)z=z1(x,y)Oxyzzc1ODz(a)(b)c2........例11..计算三重积分˝Ωxdxdydz,其中Ω为三个坐标面与平面x+2y+z=1所围成的闭区域...............如果延续刚才的截面法,我们的计算是这样的.Dz={(x,y)|x+2y≤1−z,x≥0,y≥0}={(x,y)|0≤y≤1−z−x2,0≤x≤1−z}.˚Ωxdv=ˆ10dzˆ1−z0xdxˆ1−z−x20dy=ˆ10dzˆ1−z0x·(1−z−x2)dx=ˆ10dzˆ1−z0(1−z2x−x22)dx=ˆ10(1−z4x2−x36)����1−z0dz=112ˆ10(1−z)3dz=148.这种做法没有沿着平行于yOz面来截面的做法计算简单.........例12..计算三重积分˝Ωz2dxdydz,其中Ω为椭球面x2a2+y2b2+z2c2=1所围成的空间闭区域........在柱面坐标系下计算三重积分点M的直角坐标与柱面坐标的关系为x=rcosθ,y=rsinθ,z=z.把三重积分的变量从直角坐标变换为柱面坐标的公式为˚Ωf(x,y,z)dxdydz=˚ΩF(r,θ,z)rdrdθdz,其中F(r,θ,z)=f(rcosθ,rsinθ,z),rdrdθdz为柱面坐标系中的体积元素,有时也采用ρdρdθdz这种记号........(a)(b)xOθyzP(r,θ)M(x,y,z)zrOxyzzyxMPrφθ.......在球面坐标系下计算三重积分点M的直角坐标与球面坐标的关系为x=rsinφcosθ,y=rsinφsinθ,z=rcosφ.把三重...