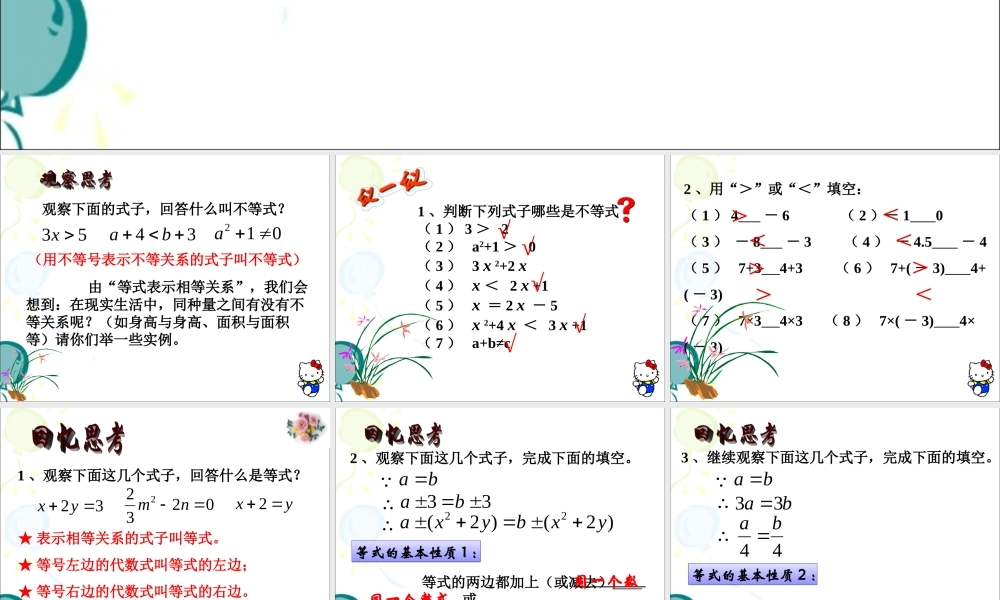
11.2不等式的基本性质观察下面的式子,回答什么叫不等式?(用不等号表示不等关系的式子叫不等式)34ba53x012a由“等式表示相等关系”,我们会想到:在现实生活中,同种量之间有没有不等关系呢?(如身高与身高、面积与面积等)请你们举一些实例。1、判断下列式子哪些是不等式(1)3>2(2)a2+1>0(3)3x2+2x(4)x<2x+1(5)x=2x-5(6)x2+4x<3x+1(7)a+b≠c√√√√√2、用“>”或“<”填空:(1)4-6(2)-10(3)-8-3(4)-4.5-4(5)7+34+3(6)7+(-3)4+(-3)(7)7×34×3(8)7×(-3)4×(-3)>>>><<<<1、观察下面这几个式子,回答什么是等式?32yx02322nmyx2★表示相等关系的式子叫等式。★等号左边的代数式叫等式的左边;★等号右边的代数式叫等式的右边。等式的两边都加上(或减去)或,所得的结果仍是等式。2、观察下面这几个式子,完成下面的填空。ba 33ba∴)2()2(22yxbyxa∴同一个数同一个整式等式的基本性质1:等式的基本性质1:3、继续观察下面这几个式子,完成下面的填空。ba ba33∴44ba∴同一个数等式的两边都乘以(或除以)(除数不能为零),所得的结果仍是等式。等式的基本性质2:等式的基本性质2:从上面的回忆可知,等式有两条基本性质,那么不等式有没有类似的性质呢?回答是肯定的,有。我们今天的主要任务就是研究不等式有哪些性质?不等式不等式的两边都加上(或减去)同一个数结果与原不等式比较不等号的方向是否改变了7>4加上512>9没有改变-3<4减去7-10<-3没有改变…………仿照下表,分组探讨仿照下表,分组探讨不等式的性质1:不等式的性质1:不等式的两边都加上(或减去)同一个数,不等号的方向不变。由上面的探讨我们可以得出:这个性质可以用数学语言表示为:ba如果,那么cacb<ba如果,那么cacb>不等式不等式的两边都乘以(或除以)同一个正数结果与原不等式比较不等号的方向是否改变了7>4乘以535>20没有改变-8<4除以4-2<1没有改变…………仿照下表,分组探讨仿照下表,分组探讨不等式的基本性质2:不等式的基本性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。由上面的探讨我们可以继续得出:ba如果,,那么bcac0cba如果,,那么bcac0c这个性质可以用数学语言表示为:1、如果x+5>4,那么两边都可得x>-12、在-7<8的两边都加上9可得。3、在5>-2的两边都减去6可得...