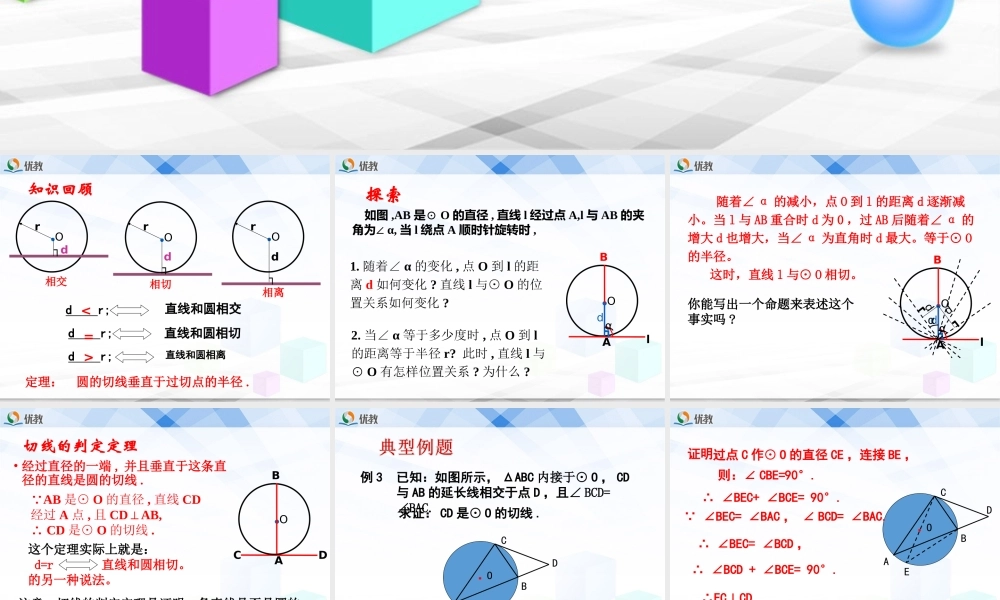
5.6直线和圆的位置关系(3)第五章圆知识回顾直线和圆相交dr;dr;直线和圆相切直线和圆相离dr;●O●O相交●O相切相离rrr┐dd┐d┐<=>定理:圆的切线垂直于过切点的半径.如图,AB是⊙O的直径,直线l经过点A,l与AB的夹角为∠α,当l绕点A顺时针旋转时,1.随着∠α的变化,点O到l的距离d如何变化?直线l与⊙O的位置关系如何变化?2.当∠α等于多少度时,点O到l的距离等于半径r?此时,直线l与⊙O有怎样位置关系?为什么?B●OAl┓dα探索随着∠α的减小,点O到l的距离d逐渐减小。当l与AB重合时d为0,过AB后随着∠α的增大d也增大,当∠α为直角时d最大。等于⊙O的半径。这时,直线l与⊙O相切。你能写出一个命题来表述这个事实吗?B●OAl┓dα┏dαd┓切线的判定定理•经过直径的一端,并且垂直于这条直径的直线是圆的切线.CDB●OA∵AB是⊙O的直径,直线CD经过A点,且CDAB,⊥∴CD是⊙O的切线.注意:切线的判定定理是证明一条直线是否是圆的切线的根据;作过切点的半径是常用经验辅助线之一.这个定理实际上就是:d=r直线和圆相切。的另一种说法。例3已知:如图所示,ΔABC内接于⊙O,CD与AB的延长线相交于点D,且∠BCD=∠BAC.求证:CD是⊙O的切线.DCBA.ODCBEA.O证明:∴CD是⊙O的切线.∴EC⊥CD.∴∠BCD+∠BCE=90°.∴∠BEC=∠BCD,∵∠BEC=∠BAC,∠BCD=∠BAC.∴∠BEC+∠BCE=90°.则:∠CBE=90°.过点C作⊙O的直径CE,连接BE,1、如图:AB是⊙O的直径,ABT=45°,∠AT=BA,求证:AT是⊙O的切线.ATB.O2、如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB,那么直线AB是⊙O的切线吗?为什么?解:直线AB是⊙O的切线.证明:连接OC。∵OA=OBAC=BC∴OCAB⊥∵直线AB经过⊙O上的点C,∴直线AB是⊙O的切线CBAO如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为点M,且l与⊙O相交于A,B两点,AB=8cm.如何沿OC所在的直线平移直线l,使l与⊙O相切?.OABCMl经过⊙O上的一点A,你能用三角尺画出⊙O的切线吗?你是怎样画的?能画出几条?与同伴进行交流.过一点如何作圆的切线?1.过圆内一点作圆的切线答.过圆内一点不能做圆的切线.3.过圆外一点能作圆的几条切线?答:能作圆的两条切线及时总结2.过圆上一点作圆的切线.已知⊙O上有一点A,过点A作出⊙O的切线.作法:答:过圆上一点能作圆的一条切线.●O●PAB作法:连接OP,以OP为直径画圆交⊙O于点A,B.作直线PA、PB则直线PA,PB为所求的切线.(3)的作法: