1.1.3 特殊角的三角函数值.pptxVIP免费

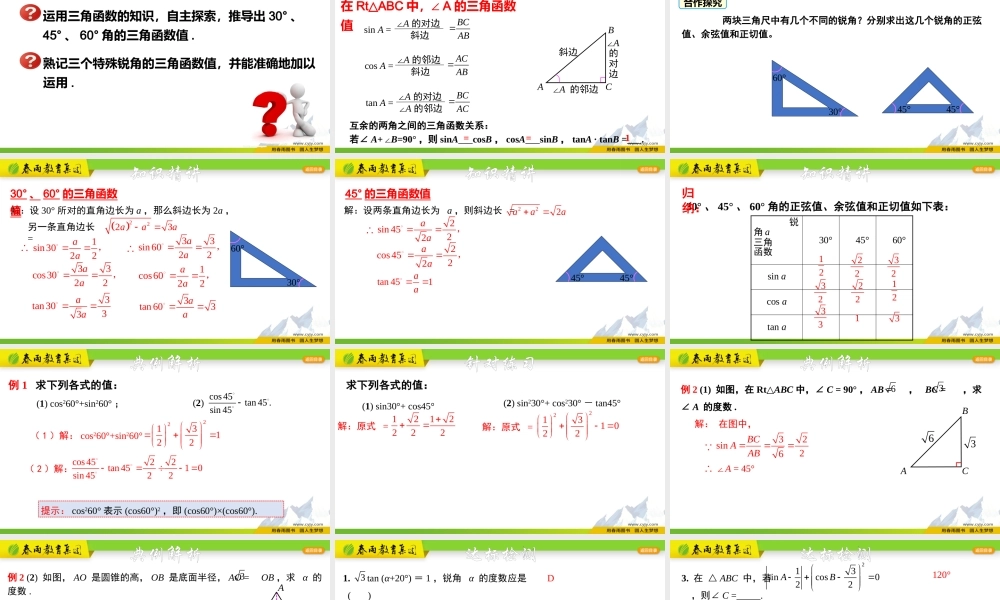
浙教版·九年级下册学习目标运用三角函数的知识，自主探索，推导出30°、45°、60°角的三角函数值.熟记三个特殊锐角的三角函数值，并能准确地加以运用.复习回顾ABC∠A的邻边∠A的对边斜边∠A的对边斜边sinA=BCAB∠A的邻边斜边cosA=ACAB∠A的对边∠A的邻边tanA=BCAC在RtABC△中，∠A的三角函数值互余的两角之间的三角函数关系：若∠A+∠B=90°，则sinAcosB，cosAsinB，tanA·tanB=.==1两块三角尺中有几个不同的锐角？分别求出这几个锐角的正弦值、余弦值和正切值。合作探究30°60°45°45°知识精讲解：设30°所对的直角边长为a，那么斜边长为2a，另一条直角边长=2223aaa33cos3022aa，3tan3033aa1sin3022aa，∴30°60°30°、60°的三角函数值知识精讲1cos6022aa，3tan603aa33sin6022aa，∴45°的三角函数值解：设两条直角边长为a，则斜边长=222aaa2cos4522aa，tan451aa2sin4522aa，∴45°45°知识精讲知识精讲30°、45°、60°角的正弦值、余弦值和正切值如下表：锐角a三角函数30°45°60°sinacosatana归纳：1232332222132123例1求下列各式的值：提示：cos260°表示(cos60°)2，即(cos60°)×(cos60°).（1）解：cos260°+sin260°2213122(1)cos260°+sin260°；典例解析(2)cos45tan45.sin45（2）解：cos4522tan4510sin4522针对练习(1)sin30°+cos45°解：原式=1212222(2)sin230°+cos230°－tan45°解：原式=22131022求下列各式的值：典例解析解：在图中，ABC36例2(1)如图，在Rt△ABC中，∠C=90°，AB=，BC=，求∠A的度数.63∴∠A=45°32sin26BCAAB 典例解析解：在图中，ABO∴α=60° tanα=33AOOBBOOB例2(2)如图，AO是圆锥的高，OB是底面半径，AO=OB，求α的度数.3达标检测1.tan(α+20°)＝1，锐角α的度数应是()A．40°B．30°C．20°D．10°D3A.cosA=B.cosA=C.tanA=1D.tanA=2.已知sinA=，则下列正确的是()1222323B达标检测3.在△ABC中，若，则∠C=.213sincos022AB120°4.如图，以O为圆心，任意长为半径画弧，与射线OA交于点B，再以B为圆心，BO长为半径画弧，两弧交于点C，画射线OC，则sinAOC∠的值为_______.32OABC达标检测5.求下列各式的值：(1)1－2sin30°cos30°(2)3tan30°－tan45°+2sin60°；解：原式=131-31-22...