28.1 第3课时 特殊角的三角函数值.pptVIP免费

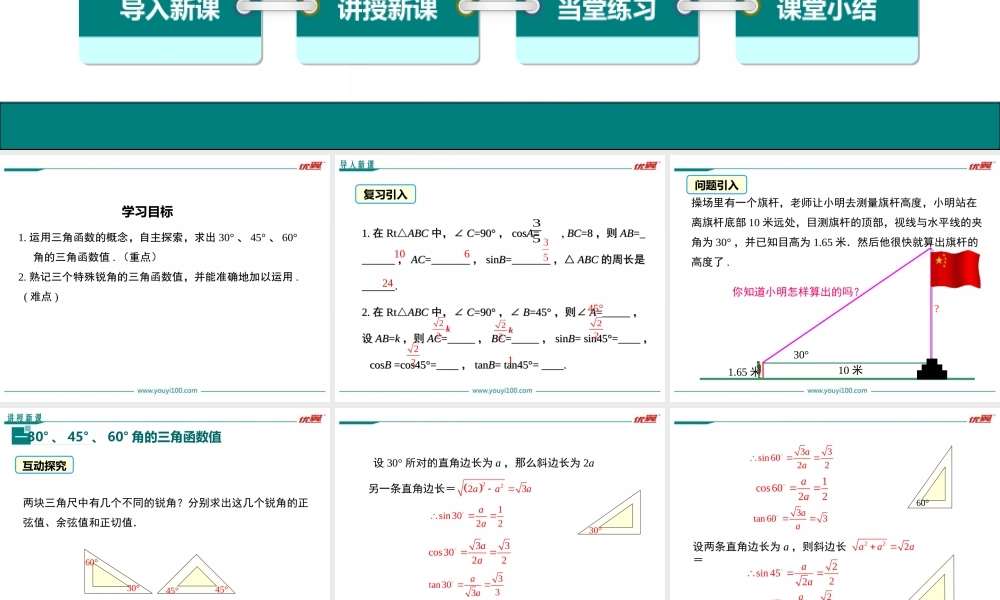
优翼课件导入新课讲授新课当堂练习课堂小结学练优九年级数学下（RJ）教学课件28.1锐角三角函数第二十八章锐角三角函数第3课时特殊角的三角函数值学习目标1.运用三角函数的概念，自主探索，求出30°、45°、60°角的三角函数值.（重点）2.熟记三个特殊锐角的三角函数值，并能准确地加以运用.(难点)导入新课复习引入1.在Rt△ABC中，∠C=90°，cosA=,BC=8，则AB=_______，AC=_______，sinB=_______，△ABC的周长是______.2.在Rt△ABC中，∠C=90°，∠B=45°，则∠A=_____，设AB=k，则AC=_____，BC=_____，sinB=sin45°=____，cosB=cos45°=____，tanB=tan45°=____.1.在Rt△ABC中，∠C=90°，cosA=,BC=8，则AB=_______，AC=_______，sinB=_______，△ABC的周长是______.2.在Rt△ABC中，∠C=90°，∠B=45°，则∠A=_____，设AB=k，则AC=_____，BC=_____，sinB=sin45°=____，cosB=cos45°=____，tanB=tan45°=____.531062445°22k22k22221操场里有一个旗杆，老师让小明去测量旗杆高度，小明站在离旗杆底部10米远处，目测旗杆的顶部，视线与水平线的夹角为30°，并已知目高为1.65米．然后他很快就算出旗杆的高度了.1.65米10米?30°你知道小明怎样算出的吗？问题引入讲授新课30°、45°、60°角的三角函数值一互动探究两块三角尺中有几个不同的锐角？分别求出这几个锐角的正弦值、余弦值和正切值．30°60°45°45°设30°所对的直角边长为a，那么斜边长为2a另一条直角边长＝2223aaa1sin3022aa33cos3022aa3tan3033aa30°33sin6022aa1cos6022aa3tan603aa设两条直角边长为a，则斜边长＝222aaa2cos4522aatan451aa2sin4522aa60°45°30°、45°、60°角的正弦值、余弦值和正切值如下表：锐角a三角函数30°45°60°sinacosatana12归纳总结典例精析例1求下列各式的值：1sin;22（）cos60+602tan.sincos45（）4545sin260°表示(sin60°)2,即(sin60°)×(sin60°).解：1sin22（）cos60+6022131;222tansincos45（）45452210.22通过三角函数值求角度二例2(1)如图，在Rt△ABC中，∠C＝90°，，求∠A的度数;3,6BCAB解：在图中，ABC36典例精析32sin,26BCAAB45;A3tan3AOOB,OBOB60.解：在图中，ABO(2)如图，AO是圆锥的高，OB是底面半径，AO=OB，求的度数.3例3已知α为锐角，且tan...