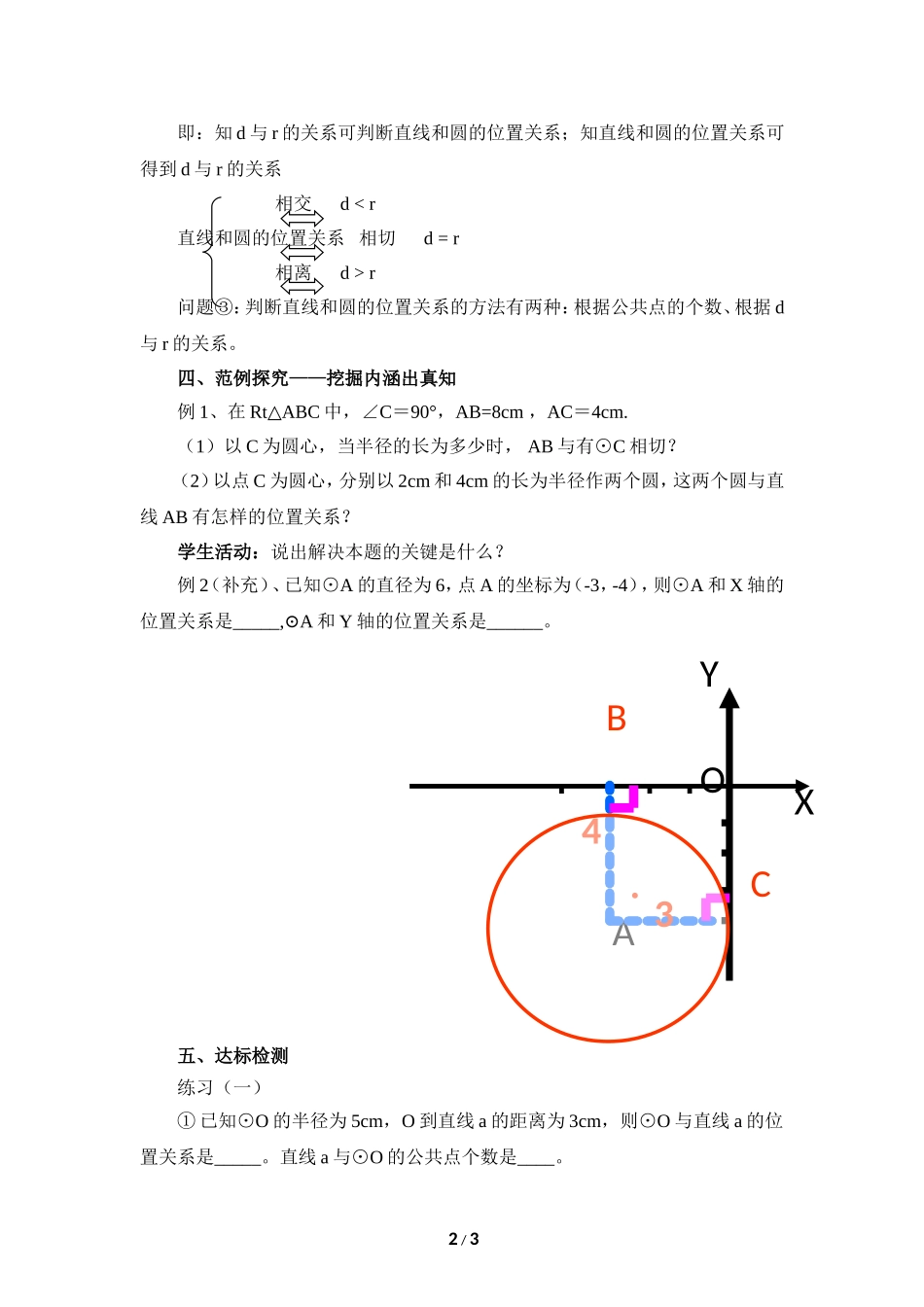
《直线和圆的位置关系(1)》导学提纲一、学海导航——提纲挈领把方向①理解直线和圆的三种位置关系并能概括其定义,会用定义来判断直线和圆的位置关系。②探究直线和圆的位置关系的数量关系及其运用。二、情境切入——激活思维现涟漪同学们,让我们闭上眼睛静静地想象:在一个夏日凉爽的早晨,我们坐在海边的沙滩上观看日出。渐渐的,太阳出来了,越来越多;慢慢的,太阳与地平线相接,一会儿,太阳完全出来了,它离开地平线越来越远,太阳升得越来越高………三、完全解读——品尝知识享盛宴请同学们自主阅读课本本节的内容,并动手探索直线和圆的位置关系及各种位置关系时的数量关系。8分钟后老师期待你的精彩回答!生生互动,展示成果:①直线和圆有哪几种位置关系?你是怎样区分这几种位置关系的?②你能用数学语言描述这三种位置关系吗?③对比点和圆的位置关系,你能否探索出圆心到直线的距离d和圆的半径r之间的数量关系?教师多媒体展示(略)拓展思考,深化知识:讨论:①直线和圆除了上述三种位置关系外,能否有第四种位置关系?直线和圆的公共点能否多于两个?②如果直线和圆的位置关系是相交、相切、相离时,一定有dr成立吗?③如何判断直线和圆的位置关系?想想看,你有几种方法?学生讨论交流,小组展示成果教师引导学生归纳:问题①:过同一直线上的三点不能做圆,所以直线和圆的交点不可能多于两个,因此不能有第四种位置关系。问题②:一定成立。故:d与r的关系与直线和圆的位置关系是互逆(等价)的。1/3即:知d与r的关系可判断直线和圆的位置关系;知直线和圆的位置关系可得到d与r的关系相交dr问题③:判断直线和圆的位置关系的方法有两种:根据公共点的个数、根据d与r的关系。四、范例探究——挖掘内涵出真知例1、在Rt△ABC中,∠C=90°,AB=8cm,AC=4cm.(1)以C为圆心,当半径的长为多少时,AB与有⊙C相切?(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与直线AB有怎样的位置关系?学生活动:说出解决本题的关键是什么?例2(补充)、已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A和X轴的位置关系是_____,⊙A和Y轴的位置关系是______。五、达标检测练习(一)①已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。2/3.AOXYBC43②已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系...