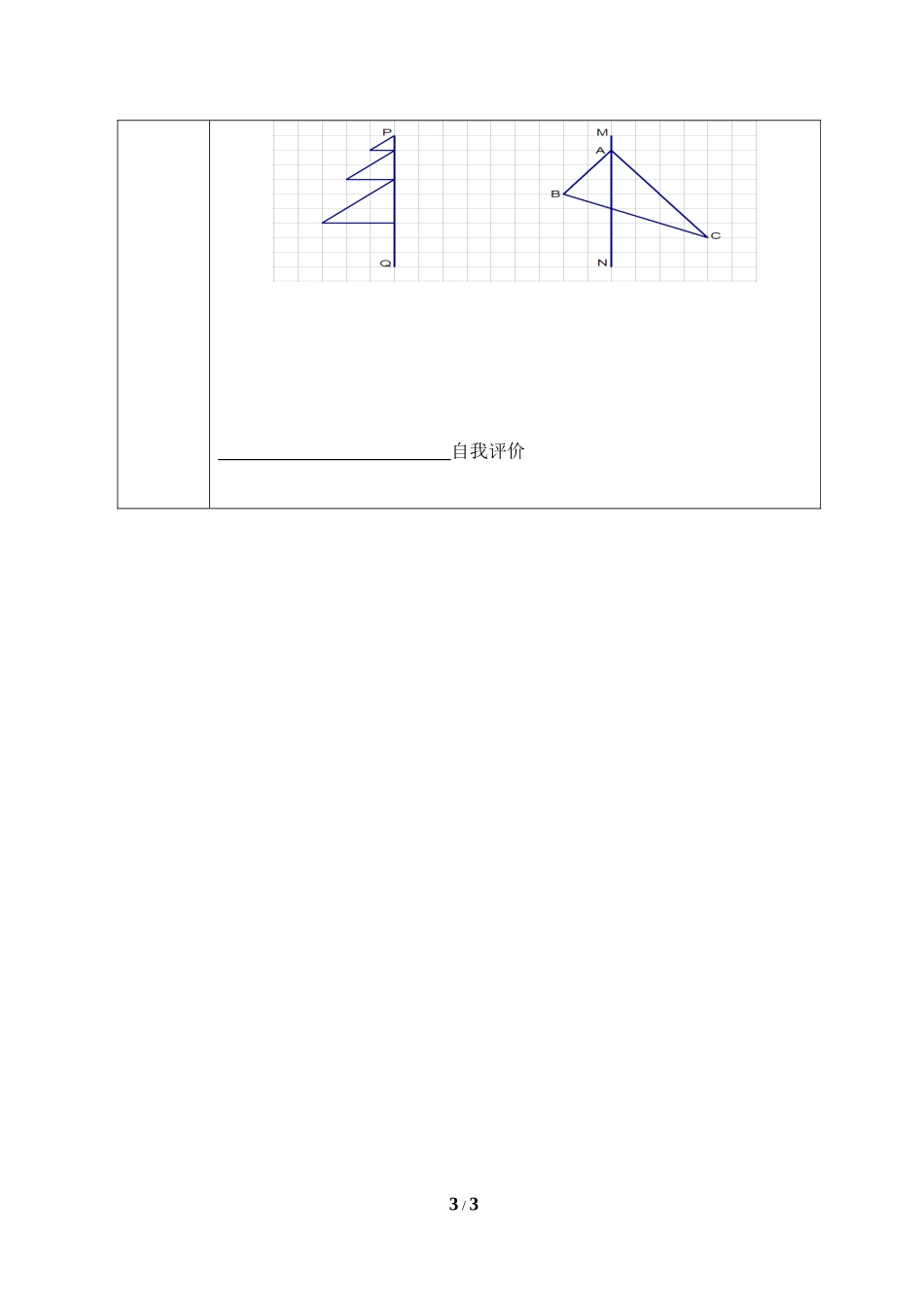
七年级数学导学案主备课题2.2探索轴对称的性质学习目标1.探索轴对称的基本性质,并结合数学实验获得性质并验证其合理性;2.会应用轴对称的性质解决一些生活中的实际问题.重点难点学习重点:探索轴对称的性质.学习难点:运用轴对称的性质解决实际问题.旧知识链接轴对称图形:成轴对称:问题探究达标检测学习过程:一、预习课本43~44页内容,思考:轴对称有哪些性质?二、探究新知:1、将一张矩形纸对折,然后用笔尖扎出“14”这个数字,然后展开铺平。(1)左图中的两个“14”有什么关系?(2)连接图中同一次扎出的两个点,如点A和A′、F和F′,用刻度尺、量角器测一测这些线段和折痕有什么关系?(4)∠1与∠2有什么关系?∠3与∠4呢?说说你的理由?2、完成43页做一做内容。3、通过以上探索可知:轴对称的性质(1)对应点的连线被对称轴;(2)对应线段;,对应角。A4、应用1:已知对称轴m和一个点A,.m要画出点A关于m的对称点A′应用2:已知对称轴l和一条线段AB,如何画出线段AB关于l的对应线段1/34321E'F'D'C'B'A'ABCDFEA′B′?.三、巩固练习(1)两个图形关于某直线对称,对称点一定()A.这直线的两旁B.这直线的同旁C.这直线上D.这直线两旁或这直线上(2)下面说法中正确的是()A.设A,B关于直线MN对称,则AB垂直平分MN。B.如果△ABC≌△DEF,则一定存在一条直线MN,使△ABC与△DEF关于MN对称。C.如果一个三角形是轴对称图形,且对称轴不止一条,则它是等边三角形。D.两个图形关于MN对称,则这两个图形分别在MN的两侧。(3)轴对称图形沿对称轴对折后,对称轴两旁的部分()A.完全重合B.不完全重合C.两者都有(4)若两个多边形成轴对称,则它们的面积,周长,相应对角线长度。(5)如果两个图形关于某条直线对称,那么对应点所连的线段被(6)右图是轴对称图形,相等的线段是,相等的角有。(7)若直角三角形是轴对称图形,则三个内角的度数为、、。(8)左图是一棵树的一半,以树干PQ为对称轴画出树的另一半;在右图中,做出△ABC关于直线MN的轴对称图形△ADE。2/3自我评价3/3