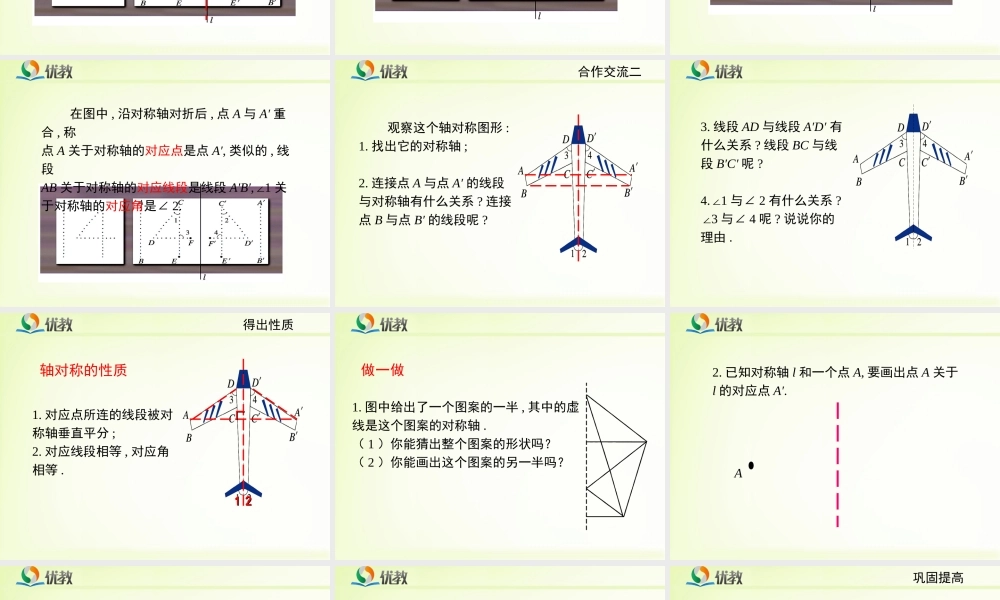
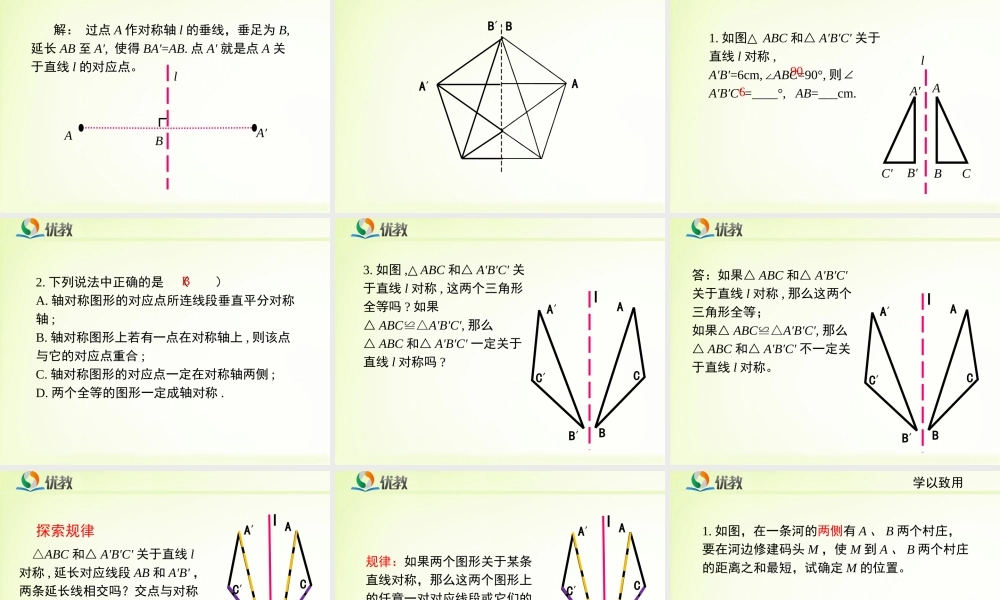
第二章轴对称2.探索轴对称的性质Contents目录01020304巩固提高反思小结合作交流一学以致用0506合作交流二得出性质实验操作:将一张矩形纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平.合作交流一1.图中,两个“14”有什么关系?2.在扎字的过程中,点E与点E′重合,点F与点F′重合.设折痕所在直线为l,连接点E与点E′的线段与l有什么关系?点F与点F′呢?3.线段AB与A′B′有什么关系?CD与C′D′呢?4.1∠与∠2有什么关系?3∠与∠4呢?说说你的理由.在图中,沿对称轴对折后,点A与A′重合,称点A关于对称轴的对应点是点A′,类似的,线段AB关于对称轴的对应线段是线段A′B′,1∠关于对称轴的对应角是∠2.观察这个轴对称图形:1.找出它的对称轴;2.连接点A与点A′的线段与对称轴有什么关系?连接点B与点B′的线段呢?合作交流二3.线段AD与线段A′D′有什么关系?线段BC与线段B′C′呢?4.1∠与∠2有什么关系?3∠与∠4呢?说说你的理由.1.对应点所连的线段被对称轴垂直平分;2.对应线段相等,对应角相等.∟∟1122轴对称的性质得出性质1.图中给出了一个图案的一半,其中的虚线是这个图案的对称轴.(1)你能猜出整个图案的形状吗?(2)你能画出这个图案的另一半吗?做一做2.已知对称轴l和一个点A,要画出点A关于l的对应点A′.AA∟∟l解:过点A作对称轴l的垂线,垂足为B,延长AB至A′,使得BA′=AB.点A′就是点A关于直线l的对应点。BA′AA′BB′1.如图△ABC和△A′B′C′关于直线l对称,A′B′=6cm,∠ABC=90°,则∠A′B′C′=____°,AB=___cm.AA′BB′CC′l906巩固提高2.下列说法中正确的是()A.轴对称图形的对应点所连线段垂直平分对称轴;B.轴对称图形上若有一点在对称轴上,则该点与它的对应点重合;C.轴对称图形的对应点一定在对称轴两侧;D.两个全等的图形一定成轴对称.B3.如图,△ABC和△A′B′C′关于直线l对称,这两个三角形全等吗?如果△ABC≌△A′B′C′,那么△ABC和△A′B′C′一定关于直线l对称吗?lAA′BB′CC′答:如果△ABC和△A′B′C′关于直线l对称,那么这两个三角形全等;如果△ABC≌△A′B′C′,那么△ABC和△A′B′C′不一定关于直线l对称。lAA′BB′CC′△ABC和△A′B′C′关于直线l对称,延长对应线段AB和A′B′,两条延长线相交吗?交点与对称轴l有什么关系?延长其他对应线段呢?再找几个成轴对称的图形观察一下,你能发现什么规律?lAA′BB′CC′探索规律lAA′BB′CC′规律:如果两个图形关于某条直线对称,那么这两个图形上的任意一对对应线段或它们的延...