21.2 二次根式的乘除 第2课时.pptVIP免费

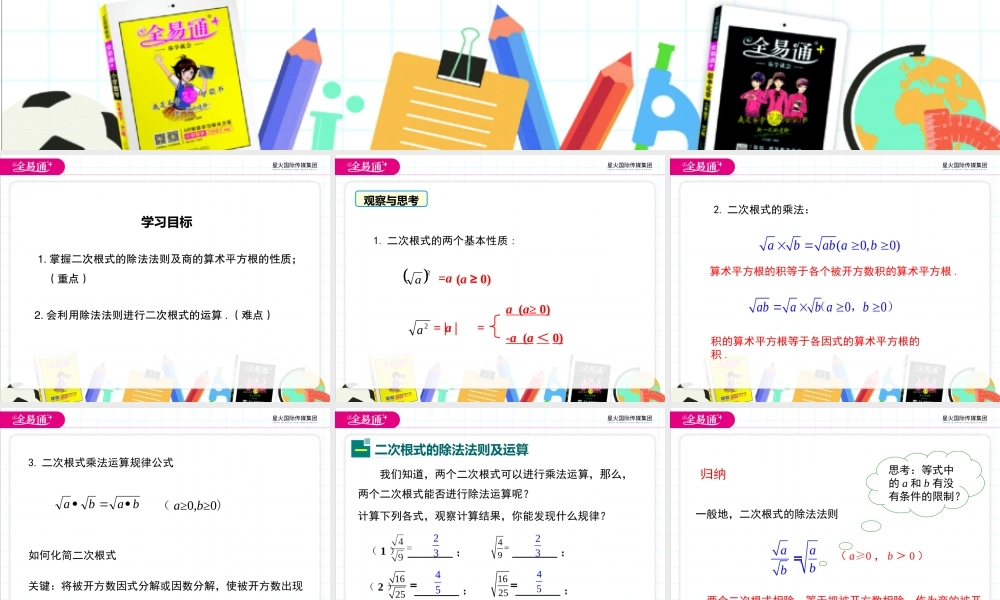
第21章二次根式21.2二次根式的乘除第2课时学习目标1.掌握二次根式的除法法则及商的算术平方根的性质；（重点）2.会利用除法法则进行二次根式的运算.（难点）1.二次根式的两个基本性质:2a=a(a≥0)2a=∣a∣a(a≥0)-a(a＜0)=观察与思考(0,0)ababab00ababab（，）2.二次根式的乘法：算术平方根的积等于各个被开方数积的算术平方根.积的算术平方根等于各因式的算术平方根的积.baba3.二次根式乘法运算规律公式（a≥0,b≥0)关键：将被开方数因式分解或因数分解，使被开方数出现“完全平方数”或“偶次方因式偶次方因式”.如何化简二次根式16162525==（2）36364949==（3）_______；_______；_______；_______；_______；_______．计算下列各式，观察计算结果，你能发现什么规律？2323454567674=9二次根式的除法法则及运算一我们知道，两个二次根式可以进行乘法运算，那么，两个二次根式能否进行除法运算呢？（1）归纳一般地，二次根式的除法法则=aabb（a≥0，b＞0）两个二次根式相除，等于把被开方数相除，作为商的被开方数.思考：等式中的a和b有没有条件的限制？解：4040(1)822;5541414(2)12164.3123123典例精析例1计算：40411;23125.aabb0,0bababa0,0ba商的算术平方根的性质及化简二baba0,0ba注意:(1)这里的被开方数是一个整式（可以是多项式，也可以是单项式）.(2)注意被开方数的取值范围.1.与积的算术平方根的性质比较：baab0,0ba共同点：一个根号变成两个根号.区别：取值范围不同.商的算术平方根:2.理解和记忆商的算术平方根要注意的问题：例2化简：（1）12(要求分母不带根号)（2）12+1(要求分母不带根号)（1）12=1•22•2=22；（2）12+1=(21)21(21)(21)解：提示：（1）要进行根式化简，关键是要搞清楚分式的分子和分母都乘什么，有时还要对分母进行化简；（2）有理化因式确定方法.如有理化因式是它本身，的有理化因式是.22121这种方法有的地方称之为分母有理化，即把分母中的根号化去的过程.例2化简3753410027333310010100解：2275535427333观察上面各数并思考：（1）你觉得这些数能否再化简，它们已经是最简二次根式了吗？（2）这些结果有什么共同特点，你认为一个二次根式满足什么条件就可以说它是最简二次根式了？156253aa，，最简二次根式的概念及判断三156253aa，，可以发现这些式子有如下两个...