《一元二次方程（1）》同步课件.pptVIP免费

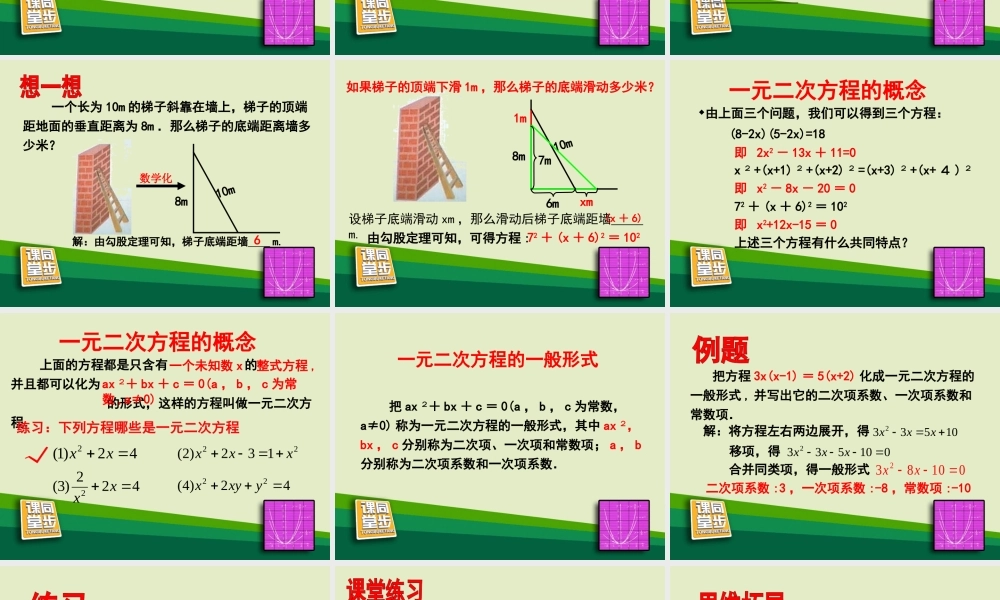
一元二次方程(1)1.在生活中，我们常用方程思想解决实际问题，步骤是：（1）把待求的量用字母表示出来（2）寻求等量关系（3）根据等量关系列方程（组）（4）解方程（组）（5）答2.整式的概念单项式和多项式统称为整式.3.完全平方公式2222)(bababa2222bababa）（幼儿园某教室矩形地面的长为8m，宽为5m，现准备在地面正中间铺设一块面积为18m2的地毯，四周未铺地毯的条形区域的宽度都相同，你能求出这个宽度吗？xxx（5－2x）8mx（8－2x)18m25m解：设花边的宽为xm,(8－2x)(5－2x)=18根据题意,可得方程观察下面等式：222221413121110你还能找到其他的五个连续整数，使前三个数的平方和等于后两个数的平方和吗？观察下面等式：设五个连续整数中的第一个数为x，那么后面四个数依次可表示为：，，，．x＋1x＋2x＋3x＋4根据题意，可得方程：(x＋1)2(x＋2)2＋(x＋3)2(x＋4)2＝＋x2＋222221413121110一个长为10m的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8m．那么梯子的底端距离墙多少米？数学化8m10m解：由勾股定理可知，梯子底端距墙m.68m10m如果梯子的顶端下滑1m，那么梯子的底端滑动多少米？1m7mxm6m设梯子底端滑动xm，那么滑动后梯子底端距墙m.(x＋6)由勾股定理可知，可得方程:72＋(x＋6)2＝102由上面三个问题，我们可以得到三个方程：(8-2x)(5-2x)=18即2x2－13x＋11=0x２+(x+1)２+(x+2)２=(x+3)２+(x+４)２即x2－8x－20＝0即x2+12x-15＝0上述三个方程有什么共同特点？一元二次方程的概念72＋(x＋6)2＝102上面的方程都是只含有的并且都可以化为的形式，这样的方程叫做一元二次方程．一个未知数x整式方程,ax２＋bx＋c＝0(a，b，c为常数,a≠0)一元二次方程的概念42)1(2xx22132)2(xxx422)3(2xx42)4(22yxyx把ax２＋bx＋c＝0(a，b，c为常数，a≠0)称为一元二次方程的一般形式，其中ax２，bx，c分别称为二次项、一次项和常数项；a，b分别称为二次项系数和一次项系数．一元二次方程的一般形式把方程3x(x-1)＝5(x+2)化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项．解：将方程左右两边展开，得010832xx二次项系数:3，一次项系数:-8，常数项:-10105332xxx0105332xxx移项，得合并同类项，得一般形式写出方程的二次项系数、一次项系数和常数项.12)3)(31(2xxx二次项系数:1，一次项系数:10，常数项:2解：将方程左边展开，得02102xx1293322...