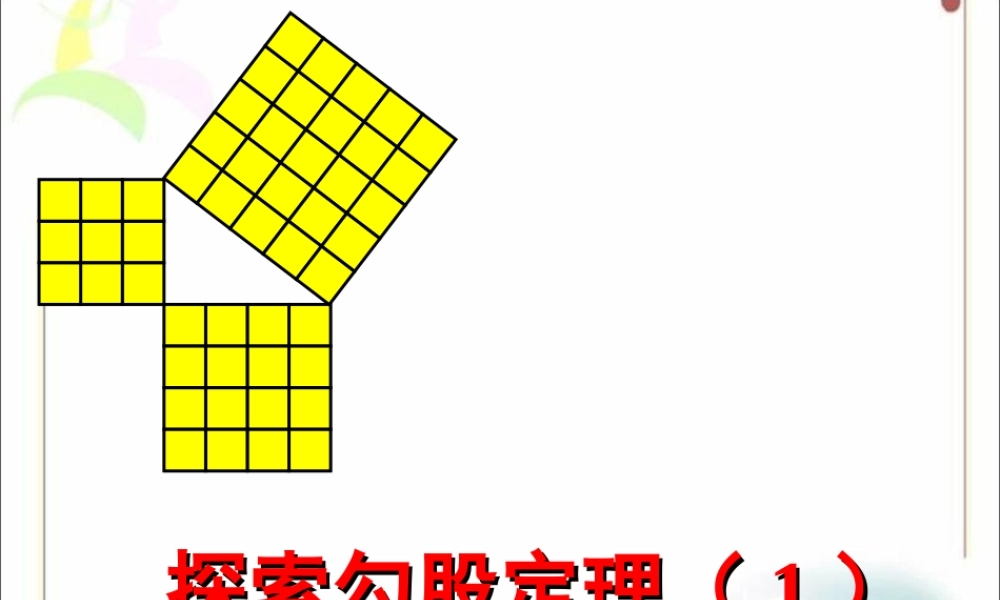
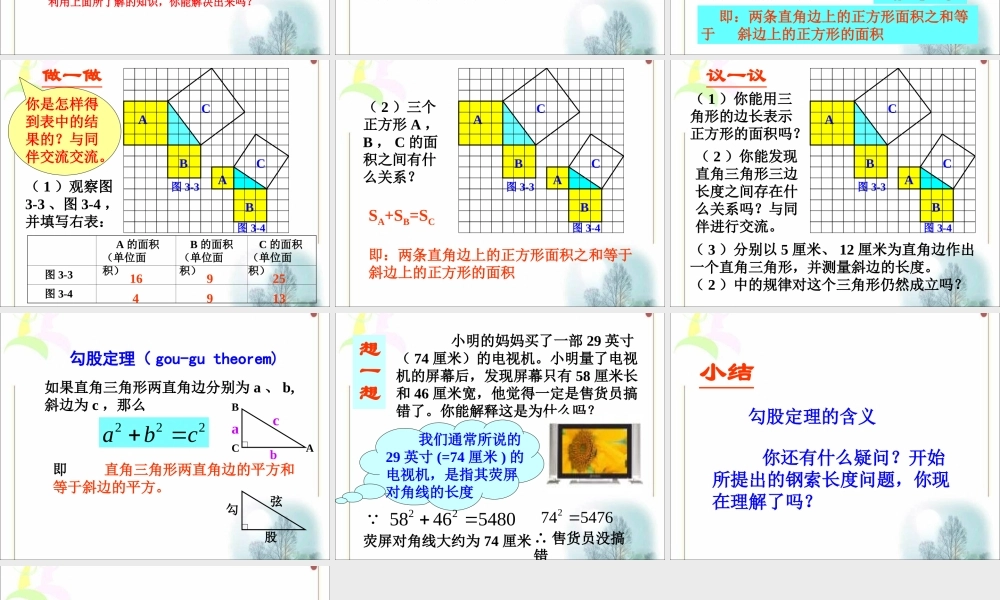
探索勾股定理(探索勾股定理(11))公元前1100年《周髀算经》中记载了西周初期,数学家商高曾与辅佐周成王的周公谈到:如果直角三角形的两个直角边分别为3和4,则这个直角三角形的斜边为5。这就是勾股定理或商高定理。在国外,相传勾股定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。法国和比利时称它为“驴桥定理”,埃及称它为“埃及三角形”等。但他们发现的时间都比我国要迟得多。希腊数学家毕达哥拉斯美国总統的证明伽菲尔德1881年成为美国第20任总统1876年提出有关证明,证法称为“总统”证法如图3-1,从电线杆离地面8米处向地面拉一钢索,若这条钢索在地面的固定点距离电线杆底部6米,那么需要多长的钢索?图3-1利用上面所了解的知识,你能解决出来吗?ABCABC(图中每个小方格代表一个单位面积)图3-1图3-2(1)观察图3-1正方形A中含有个小方格,即A的面积是个单位面积。正方形B的面积是个单位面积。正方形C的面积是个单位面积。99918ABCABC(图中每个小方格代表一个单位面积)图3-1图3-2(2)在图3-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图3-1中三个正方形A,B,C的面积之间有什么关系吗?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积ABC图3-3ABC图3-4(1)观察图3-3、图3-4,并填写右表:A的面积(单位面积)B的面积(单位面积)C的面积(单位面积)图3-3图3-4169254913你是怎样得到表中的结果的?与同伴交流交流。做一做ABC图3-3ABC图3-4(2)三个正方形A,B,C的面积之间有什么关系?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积ABC图3-3ABC图3-4(1)你能用三角形的边长表示正方形的面积吗?(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度。(2)中的规律对这个三角形仍然成立吗?议一议勾股定理(gou-gutheorem)如果直角三角形两直角边分别为a、b,斜边为c,那么222abc即直角三角形两直角边的平方和等于斜边的平方。abc勾股弦ABC小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?我们通常所说的29英寸(=74厘米)的电视机,是指其荧屏对角线的长度27454762258465480∴售货员没搞错 ...