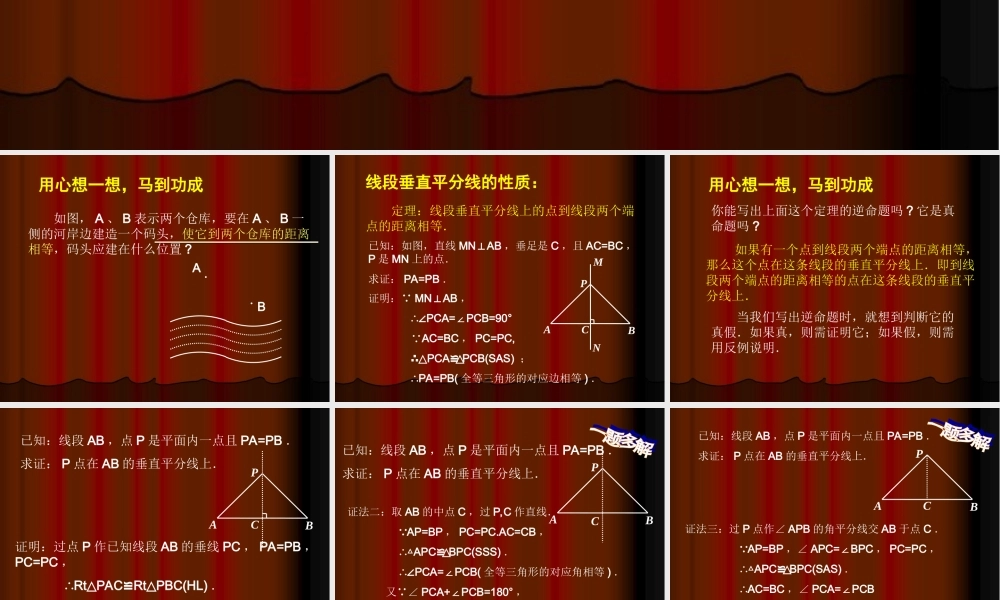
第四节线段的垂直平分线(一)用心想一想,马到功成如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建在什么位置?AB线段垂直平分线的性质:定理:线段垂直平分线上的点到线段两个端点的距离相等.已知:如图,直线MNAB⊥,垂足是C,且AC=BC,P是MN上的点.求证:PA=PB.NAPBCM证明: MNAB⊥,∴∠PCA=PCB=90°∠ AC=BC,PC=PC,∴△PCAPCB(SAS)≌△;∴PA=PB(全等三角形的对应边相等).用心想一想,马到功成你能写出上面这个定理的逆命题吗?它是真命题吗?如果有一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上.即到线段两个端点的距离相等的点在这条线段的垂直平分线上.当我们写出逆命题时,就想到判断它的真假.如果真,则需证明它;如果假,则需用反例说明.已知:线段AB,点P是平面内一点且PA=PB.求证:P点在AB的垂直平分线上.证明:过点P作已知线段AB的垂线PC,PA=PB,PC=PC,∴RtPACRtPBC(HL)△≌△.∴AC=BC,即P点在AB的垂直平分线上.CBPA证法二:取AB的中点C,过P,C作直线. AP=BP,PC=PC.AC=CB,∴△APCBPC(SSS)≌△.∴∠PCA=PCB(∠全等三角形的对应角相等).又 ∠PCA+PCB=180°∠,∴∠PCA=PCB=90°∠∠,即PCAB⊥∴P点在AB的垂直平分线上.CBPA已知:线段AB,点P是平面内一点且PA=PB.求证:P点在AB的垂直平分线上.CBPA已知:线段AB,点P是平面内一点且PA=PB.求证:P点在AB的垂直平分线上.证法三:过P点作∠APB的角平分线交AB于点C. AP=BP,∠APC=BPC∠,PC=PC,∴△APCBPC(SAS)≌△.∴AC=BC,∠PCA=PCB∠又 ∠PCA+PCB=180°PCA=PCB=90°∠∴∠∠∴P点在线段AB的垂直平分线上.线段垂直平分线的判定:定理:到线段两个端点的距离相等的点在这条线段的垂直平分线上.练一练已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC.求证:直线AO垂直平分线段BC.证明: AB=AC,∴点A在线段BC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).同理,点O在线段BC的垂直平分线上.∴直线AO是线段BC的垂直平分线(两点确定一条直线).你还有其他证明方法吗?加强应用在RtABC△中,∠B=90°,∠A=40°,AC的垂直平分线MN与AB相交于点D,则∠BCD的度数是多少?ABCDMN分析:由点D在线段AC的垂直平分线上,可以得到DA=DC,即△DAC是等腰三角形,问题解决.解: 点D在线段AC的垂直平分线上,∴DA=DC,∴∠DAC=∠A=40° ∠B=90°...